Funzione di produzione

La funzione di produzione è la relazione tra la quantità di produzione di un bene economico ( prodotto o output ) e le quantità dei singoli fattori di produzione ( input ). La funzione di produzione è uno strumento utilizzato in microeconomia ( economia politica ) per studiare le scelte di produzione. È una funzione matematica che mette in relazione il flusso di un bene prodotto Y ( output ) e il flusso degli n fattori produttivi X ( input ) utilizzati nel processo produttivo in un determinato periodo di tempo.

Y = f ( x₁ , x₂, x₃, ... , x_n)

Dato un insieme di produzione Z, la funzione di produzione associa la quantità massima di produzione ottenibile con una determinata combinazione di quantità dei fattori produttivi, in un determinato periodo di tempo, a parità di capitale. Nel caso più semplice di un prodotto Y e di un fattore X la funzione di produzione è formulata nel seguente modo:

Y_q = f ( x_q )

La funzione di produzione di un prodotto e un fattore produttivo è facilmente rappresentabile sul piano cartesiano ponendo la quantità della produzione Y sull'asse delle ordinate e la quantità del fattore produttivo X sull'asse delle ascisse. La rappresentazione grafica della funzione di produzione è anche detta curva di produzione.

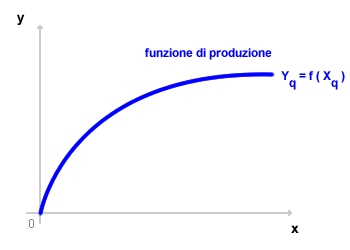
Nella rappresentazione grafica la funzione di produzione coincide con la frontiera dell'insieme di produzione. La funzione di produzione è associata al processo produttivo dell'insieme di produzione che consente di massimizzare l'output Y per ogni livello di input X. Dal punto di vista matematico la funzione di produzione ha le seguenti proprietà:

• Funzione continua. Una funzione di produzione è una funzione continua poiché sia il prodotto Y ( output ) che il fattore produttivo X ( input ) sono perfettamente divisibili.
• Funzione monotona. Una funzione di produzione è una funzione monotona poiché la quantità di produzione ( output ) è sempre in funzione non decrescente della quantità del fattore produttivo impiegato ( input ).

La rappresentazione grafica della funzione di produzione varia a seconda dei rendimenti di scala della produzione. La funzione di produzione può avere rendimenti decrescenti ( grafico precedente ), rendimenti costanti o rendimenti crescenti. I rendimenti di scala sono costanti se la produzione varia nella stessa proporzione dell'impiego dei fattori produttivi. Sono rendimenti crescenti se la produzione aumenta in modo più che proporzionale all'incremento di impiego del fattore produttivo. Sono rendimenti decrescenti se la produzione aumenta in modo meno che proporzionale all'incremento di impiego del fattore produttivo. Nel caso dei rendimenti di scala crescenti la funzione di produzione può essere rappresentata nel seguente modo:

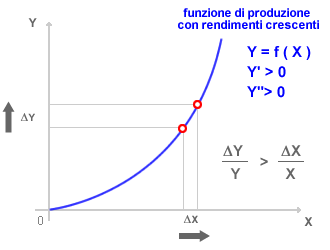
Funzione omogenea. Per una rappresentazione elementare della funzione di produzione in relazione ai diversi rendimenti di scala si può utilizzare una funzione omogenea di grado k. Il grado di omogeneità k della funzione matematica permette la rappresentazione cartesiana della funzione di produzione nel caso dei rendimenti di scala costanti ( k = 1 ), dei rendimenti crescenti crescenti ( k > 0 ) o dei rendimenti decrescenti ( k < 1 ).

Breve periodo. La funzione di produzione misura la relazione tra produzione e fattori nel breve periodo, considerando costanti il capitale e la tecnologia degli impianti produttivi a disposizione dell'impresa. È quindi una curva di produzione statica. L'imprenditore può soltanto variare la quantità di utilizzo dei fattori produttivi. Non può modificare né la capacità produttiva degli impianti, né la tecnologia di produzione. Le possibili combinazioni dei fattori produttivi sono costanti e sono delimitate dalla frontiera della curva di produzione.

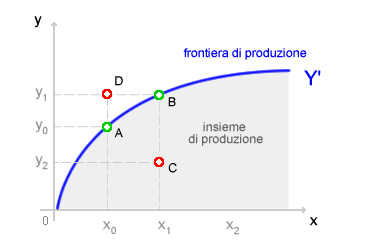
Ad esempio, nella funzione di produzione precedente i punti A e B sono situati sulla frontiera di produzione e sono combinazioni efficienti poiché, a parità di utilizzo del fattore produttivo ( x ), consentono di massimizzare la produzione ( y ). Il punto C è anch'esso compreso nell'insieme della produzione, può essere realizzato dall'impresa, ma si tratta di una situazione di inefficienza, poiché a parità di utilizzo del fattore produttivo ( x₁ ) si ottiene una quantità di prodotto ( y₂ ) inferiore rispetto alla frontiera di produzione ( y₁ ). Il punto D, invece, non è tecnicamente realizzabile in quanto è situato al di fuori della frontiera di produzione.

Progresso tecnologico. Nel lungo periodo l'impresa può modificare la capacità degli impianti e la tecnologia di produzione, adottando le innovazioni tecnologiche rese possibili dal progresso tecnico-scientifico. Nel lungo periodo, pertanto, la funzione di produzione subisce radicali variazioni di inclinazione e di posizione. Dal punto di vosta grafico, ipotizzando che il progresso aumenti la produttività e l'efficienza degli impianti, la funzione di produzione si trasforma in una curva dinamica e si sposta verso l'alto ( traslazione verticale ).

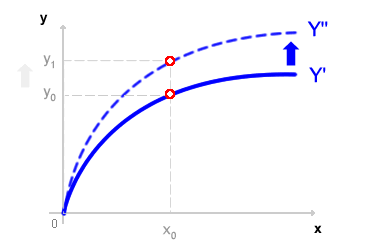
Le innovazioni tecnologiche consentono di ottenere una quantità maggiore di prodotto a parità di utilizzo delle quantità di fattori e/o un minore utilizzo delle quantità di fattori produttivi per produrre una determinata quantità di prodotto ( efficienza produttiva ).