Isoquanto
L'isoquanto è l'insieme delle diverse combinazioni dei fattori produttivi ( input ) che consentono di produrre la stessa quantità di produzione totale ( output ). Gli isoquanti sono detti anche isoquanti di produzione e sono utilizzati in economia politica nella teoria dell'impresa. Il termine isoquanto è composto dall'unione delle parole "iso" ( stessa ) e "quantità" ( di prodotto ). Nel caso di una funzione di produzione a due variabili ( fattori produttivi ) l'isoquanto può essere rappresentato sul piano cartesiano indicando sull'asse delle ascisse la quantità del primo fattore produttivo (x1) e sull'asse delle ordinate il secondo fattore produttivo (x2). Le diverse combinazioni delle quantità dei fattori (x1, x2) sono rappresentate sul piano sotto forma di punti alle coordinate (x,y). Una curva di isoquanto raggruppa tutte le combinazioni (x1, x2) dei fattori che consentono di produrre la stessa quantità di prodotto (y).Sul piano le combinazioni dei fattori a parità di prodotto assumono la forma di una curva detta curva di isoquanto.
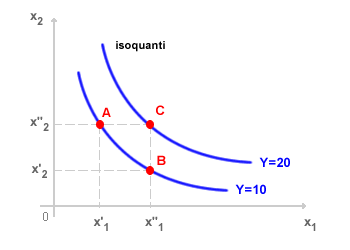
Ogni curva di isoquanto è associata a un livello di produzione differente. Gli isoquanti più vicini all'origine sono associati a un livello di produzione più basso, quelli più esterni a un livello di produzione più alto. Le curve di isoquanto sono inclinate negativamente e sono convesse verso l'origine degli assi, al pari di quanto già visto nelle curve di indifferenza nella teoria del consumatore, poiché le combinazioni intermedie dei fattori implicano generalmente una migliore organizzazione e produttività. Per diminuire la quantità di uno dei fattori produttivi, lasciando invariata la produzione totale, è necessario aumentare la quantità impiegata dell'altro fattore produttivo. Il rapporto tra le quantità dei fattori produttivi in ogni punto della curva di isoquanto è detta saggio marginale di sostituzione tecnica. Il saggio marginale di sostituzione tecnica è il rapporto tra la variazione della quantità impiegata di un fattore produttivo (x1) e la variazione della quantità impiegata dell'altro fattore (x2), a parità di produzione finale (y).
Produttività dei fattori e saggio marginale di sostituzione tecnica. Tra il saggio marginale di sostituzione tecnica e la produttività dei fattori marginali esiste una relazione inversa di equivalenza. In una curva di isoquanto la produzione è costante ( Δy=0 ), è quindi necessario che la variazione positiva di un fattore produttivo ( +Δx1 ) sia compensata dalla variazione negativa ( -Δx2 ) dell'altro fattore produttivo. Per mantenere immutata la produzione finale ( Δy=0 ) è necessario considerare, oltre alle variazioni quantitative dei fattori produttivi ( +Δx1 , -Δx2 ), anche la produttività marginale degli stessi. Con pochi passaggi algebrici è possibile dimostrare la relazione inversa di equivalenza. Ad esempio, supposta la possibilità che una medesima quantità di prodotto ( y ) è ottenibile mediante diverse combinazioni dei fattori capitale ( K ) e lavoro ( L ), è possibile dimostrare l'equivalenza tra il saggio marginale di sostituzione tecnica e il rapporto inverso tra le produttività dei fattori nel seguente modo:
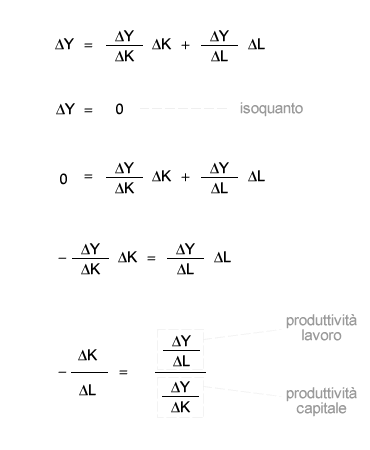
Il rapporto -ΔK/ΔL rappresenta il saggio marginale di sostituzione tecnica dei fattori produttivi capitale (K) e lavoro (L). La riduzione della quantità impiegata del fattore lavoro ( -ΔK ) genera una riduzione della produzione ( -ΔY = ΔK · PMA,K) pari all'incremento della produzione ottenuto dall'aumento della quantità impiegata dell'altro fattore produttivo ( +ΔY = ΔL · PMA,L). Dove PMA,K e PMA,L sono rispettivamente la produttività marginale del capitale ( ΔY/ΔK ) e del lavoro ( ΔY/ΔL ).
- PMA,K ΔK = PMA,L ΔL
Se così non fosse si registrerebbe un aumento ( Δy>0 ) o una diminuzione ( Δy<0 ) della produzione. È quindi possibile affermare che il rapporto tra le quantità dei fattori produttivi ( ΔK/ΔL ) è uguale al rapporto inverso tra le produttività marginali del lavoro ( ΔY/ΔL ) e del capitale ( ΔY/ΔK ).
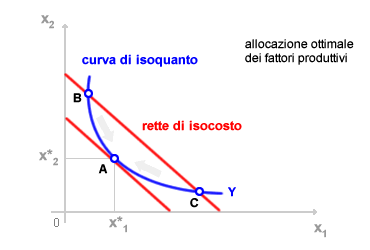
Allocazione ottimale dei fattori produttivi. Le curve di isoquanto sono un elemento fondamentale per determinare l'allocazione ottimale dei fattori produttivi. La combinazione ottimale dei fattori è determinata dall'uguaglianza del saggio marginale di sostituzione tecnica ( pendenza della curva di isoquanto ) con il saggio marginale di trasformazione ( pendenza della retta di isocosto ).
