Isocosto
Un isocosto è l'insieme delle combinazioni di due fattori produttivi che determinano lo stesso costo di produzione complessivo. Dati i prezzi dei fattori produttivi (w1/w2 ), l'isocosto della produzione individua le combinazioni acquistabili dei due fattori produttivi ( x1, x2 ) che consentono di mantenere costante il costo totale della produzione ( C ). L'equazione di isocosto può essere rappresentata graficamente sul piano cartesiano. Nei casi più semplici è solitamente una retta ( retta di isocosto ). Nei casi più complessi può anche assumere forme curve e non lineari ( curva di isocosto ). In una retta di isocosto il costo totale della produzione è costante al variare delle combinazioni delle quantità di utilizzo dei fattori produttivi. Le rette di isocosto più esterne sono associate a costi di produzione maggiori. Viceversa, quelle più interne sono associate a costi di produzione minori. Ad esempio, nel diagramma seguente sono rappresentate due rette di isocosto, la prima è associata al costo di produzione C e la seconda al costo di produzione C', dove C > C'.
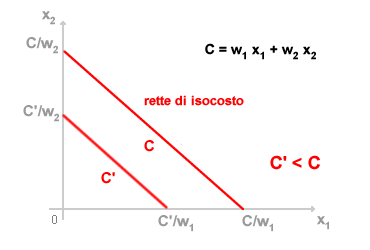
L'intercetta delle rette di isocosto sull'asse del diagramma è la quantità massima di impiego del fattore produttivo indicato nell'asse di riferimento. Ad esempio, dato un costo totale C e due fattori produttivi X1 e X2 con relativi costi pari a w1 e w2, l'intercetta sull'asse X1 è individuata dal rapporto C/w1 mentre l'intercetta sull'asse X2 è individuata dal rapporto C/w2. La pendenza della retta di isocosto è pari al valore assoluto del rapporto tra i costi dei fattori produttivi w1 / w2 ed è detta saggio marginale di trasformazione. Una famiglia di isocosti è un insieme di rette di isocosto associate ciascuna a un differente livello di costo totale.
Esempio di isocosto. Data una funzione di produzione con due fattori produttivi ( capitale e lavoro ) e dati i prezzi dei fattori produttivi ( pK=3, pL=2 ), le seguenti combinazioni di quantità dei fattori consentono di mantenere costante il costo totale della produzione. Sono pertanto delle combinazioni appartenenti al medesimo isocosto.
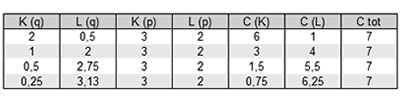
Ad esempio, due unità di capitale K e 0,5 unità di lavoro L ( mezza giornata di un lavoratore ) implicano per l'impresa un costo totale C pari a 7. Il costo del capitale CK è pari a (2·3=6) mentre il costo del lavoro CL è pari a (0,5·2=1) . Lo stesso costo totale ( C=7 ) si ottiene utilizzando un'unità di capitale ( K=1 ) e due unità di lavoro ( L=2 ). In questa seconda combinazione di fattori il costo del capitale CK è pari a (1·3=3) mentre il costo del lavoro CL è pari a (2·2=4). Sommando il costo del capitale CK e il costo del lavoro CL si ottiene un costo totale pari a sette (C=CK+CL=3+4=7).
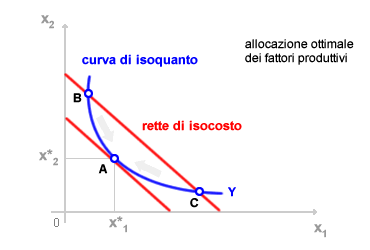
Allocazione ottimale dei fattori produttivi. Le rette di isocosto sono un elemento fondamentale per individuare l'allocazione ottimale dei fattori produttivi nella produzione. L'equilibrio ottimale è determinato dall'uguaglianza del saggio marginale di trasformazione ( pendenza della retta di isocosto ) con il saggio marginale di sostituzione tecnica ( pendenza della curva di isoquanto ).
