Sottoinsieme
Dati due insiemi A e B si dice che l'insieme A è sottoinsieme dell'insieme B se tutti gli elementi dell'insieme A appartengono anche all'insieme B.
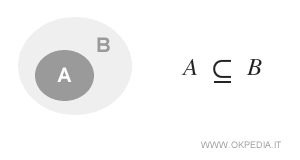
In tale caso l'insieme A è contenuto interamente nell'insieme B.
Nella notazione matematica si scrive A ⊆ B e si legge "l'insieme A è sottoinsieme di B" oppure "l'insieme A è incluso in B".
Un esempio pratico
Il sottoinsieme può essere rappresentato graficamente nel seguente modo:
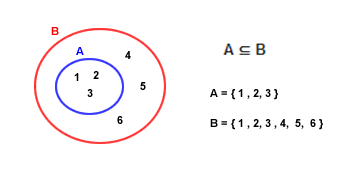
Nella rappresentazione grafica sono presenti due insiemi A e B.
- L'insieme A è composto dagli elementi { 1, 2, 3 }.
- L'insieme B è composto dagli elementi { 1, 2, 3, 4, 5, 6 }.
Come si può facilmente osservare graficamente, l'insieme A è contenuto nell'insieme B. In altri termini l'insieme A è un sottoinsieme di B.
Differenza tra inclusione normale o stretta
La relazione di inclusione del sottoinsieme può essere normale o stretta.
- Inclusione normale ( A⊆B )
Nella relazione di inclusione normale è ammessa anche l'ipotesi di uguaglianza tra gli insiemi (A=B). I due insiemi potrebbero anche coincidere.
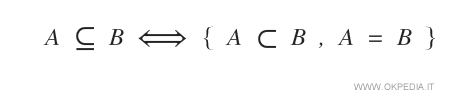
Un sottoinsieme con relazione di inclusione normale è detto- sottoinsieme proprio se i due insiemi sono diversi (A≠B)
- sottoinsieme improprio se i due insiemi sono uguali (A=B) o il sottoinsieme è un insieme vuoto (A=ø).
Un esempio pratico
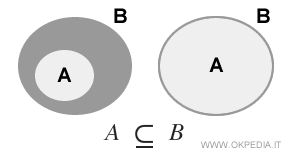
- Inclusione stretta ( A⊂B )
Nella relazione di inclusione stretta è esclusa l'ipotesi di uguaglianza degli insiemi. I due insiemi sono diversi (A≠B). Pertanto, esistono elementi dell'insieme B che non sono inclusi nell'insieme A. In tali casi si dice che "l'insieme A è incluso strettamente in B" oppure "l'insieme A è contenuto strettamente in B" e si scrive A ⊂ B.
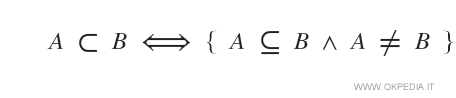
Un sottoinsieme non vuoto con relazione di inclusione stretta è sempre un sottoinsieme proprio, perché i due insiemi sono diversi.
Un esempio pratico
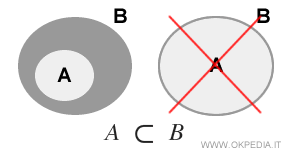
Nota. L'inclusione stretta (A⊂B) è sempre anche un'inclusione normale (A⊆B). Viceversa, l'inclusione normale (A⊆B) non è detto che sia anche un'inclusione stretta (A⊂B) perché i due insiemi potrebbero coincidere.
