Differenza insiemi
La differenza tra gli insiemi è una delle operazioni fondamentali della teoria degli insiemi. Dati due insiemi A e B, la differenza tra i due insiemi è uguale all'insieme degli elementi di A che non appartengono anche a B. L'operazione di differenza si legge "A meno B" e può essere scritta nel seguente modo:
A - B = { x | x ∈ A e x ∉ B )
La differenza tra due insiemi può essere rappresentata anche Utilizzando il metodo grafico di Eulero-Venn degli insiemi. L'insieme differenza di A meno B è l'area di colore grigio all'interno dell'insieme A.
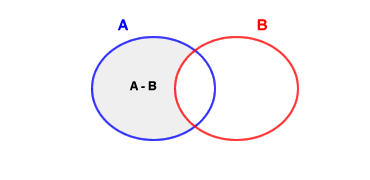
La differenza degli insiemi può essere effettuata anche se i due insiemi sono disgiunti ossia se non hanno nessun elemento in comune. In tale caso, dati due insiemi disgiunti A e B, la differenza A meno B eguaglia l'insieme A. Un esempio di differenza di insiemi disgiunti è il seguente.
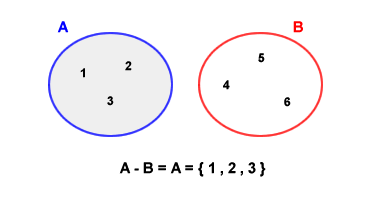
Se uno dei due insiemi è sottoinsieme dell'altro, la differenza è diversa a seconda se il primo insieme è il sottoinsieme del secondo oppure l'inverso. Ad esempio, dati due insiemi A e B tale che B ⊆ A allora l'insieme differenza A - B è uguale all'insieme complementare di B rispetto ad A. Anche caso è rappresentabile graficamente tramite il metodo Eulero-Venn. L'insieme complementare di B è l'area grigia all'interno dell'insieme A.
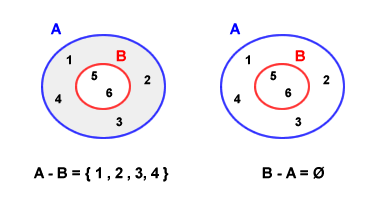
Viceversa, la differenza B - A restituisce come risultato un insieme vuoto ( Ø ) poiché non esiste alcun elemento dell'insieme B a non essere contenuto anche nell'insieme A.
 Proprietà commutativa. A differenza delle operazioni di intersezione e di unione della teoria degli insiemi, la differenza tra insiemi non gode della proprietà commutativa. Dati due insiemi non uguali A ≠ B, l'insieme differenza A meno B ( A - B ) è sempre diverso dall'insieme B meno A ( A - B ). Nella differenza la proprietà commutativa è soddisfatta soltanto nel caso A = B ossia nel caso eccezionale in cui gli insiemi siano coincidenti e uguali tra loro ( insiemi uguali ). In quest'ultimo caso il risultato della differenza è sempre pari a un insieme vuoto indipendentemente dall'ordine degli insiemi.
Proprietà commutativa. A differenza delle operazioni di intersezione e di unione della teoria degli insiemi, la differenza tra insiemi non gode della proprietà commutativa. Dati due insiemi non uguali A ≠ B, l'insieme differenza A meno B ( A - B ) è sempre diverso dall'insieme B meno A ( A - B ). Nella differenza la proprietà commutativa è soddisfatta soltanto nel caso A = B ossia nel caso eccezionale in cui gli insiemi siano coincidenti e uguali tra loro ( insiemi uguali ). In quest'ultimo caso il risultato della differenza è sempre pari a un insieme vuoto indipendentemente dall'ordine degli insiemi.
