Insiemi
Un insieme è definito come una collezione di oggetti, specificata da un criterio chiaro e oggettivo che determina senza ambiguità se un dato oggetto appartiene o meno a tale insieme. Gli oggetti contenuti in un insieme sono chiamati elementi.
Un insieme matematico è generalmente rappresentato da una lettera maiuscola dell'alfabeto greco o latino ( A, B, C, ... ). Gli elementi di un insieme sono generalmente rappresentati dalle lettere minuscole dell'alfabeto greco o latino ( a, b, c, ... ) tra due parentesi graffe.
$$ A = \{ 1, 2, 3, 4, 5, ... \} $$
Ogni elemento dell'insieme compare una sola volta e, a differenza dei vettori e degli insiemi ordinati, non ha un ordine di comparizione.
Il simbolo "∈" è impiegato per indicare l'appartenenza di un oggetto/elemento a un insieme. Al contrario, quando un oggetto non appartiene a un insieme, utilizziamo il simbolo "∉".
Esempio. Immaginiamo di avere un insieme A che rappresenta i numeri interi positivi minori di 5 $$ A = \{1, 2, 3, 4\} $$ In questo esempio l'insieme A è composto da cinque elementi. Se prendiamo gli elementi p=3 e q=5 possiamo affermare che: $$ p ∈ A $$ $$ q ∉ A $$ Questo esprime chiaramente che il numero 3 è contenuto nell'insieme A, mentre il numero 5 no. Se volessimo esaminare anche un altro elemento, diciamo r=2, potremmo utilizzare la notazione compatta per indicare che sia p che r appartengono all'insieme A $$ p, r ∈ A $$
Il criterio di appartenenza degli insiemi
L'insieme è definito da un criterio di appartenenza che definisce in modo inequivocabile se un oggetto appartiene o non appartiene ad un insieme. Il criterio di appartenenza a un insieme è indicato con il simbolo ∈. L'appartenenza di un elemento x all'insieme Y è scritto "x ∈ Y" e si legge "x appartiene a Y".
$$ x \in Y $$
Allo stesso modo è possibile indicare il criterio di non appartenenza all'insieme mediante il simbolo sbarrato ∉. La non appartenenza dell'elemento x all'insieme Z è scritto "x ∉ Z" e si legge "x non appartiene a Z".
$$ x \not \in Z $$
Quando si definisce un insieme matematico, esistono diverse notazioni e rappresentazioni per specificare chiaramente i suoi elementi.
La rappresentazione dell'insieme
La rappresentazione grafica si basa sull'utlizzo dei diagrammi di Eulero-Venn, che illustrano le relazioni di inclusione e intersezione tra vari insiemi attraverso cerchi o altre forme che si sovrappongono. Questi diagrammi sono utili per visualizzare chiaramente le relazioni tra insiemi in modo intuitivo e immediato..
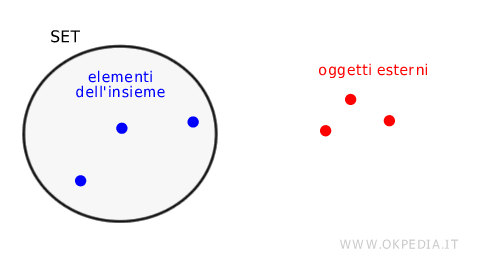
Oltre alla rappresentazione grafica esistono anche altre rappresentazione come la rappresentazione tabulare, per elencazione, per proprietà caratteristica, ecc.
- Notazione formale
Utilizziamo un criterio di appartenenza per specificare gli elementi dell'insieme. Ad esempio, questa espressione, \( x \in \mathbb{N} \) indica che \( x \) è un numero naturale, e \( x < 100 \) specifica che \( x \) deve essere minore di 100. $$ A = \{ x \in \mathbb{N} : x < 100 \} $$ Questo insieme include tutti i numeri naturali da 0 fino a 99. - Notazione enumerativa
Questo metodo elenca direttamente gli elementi dell'insieme. È particolarmente utile quando l'insieme ha un numero limitato di elementi facilmente elencabili. Ad esempio, un insieme composto dai numeri naturali minori di 100 può essere scritta anche in questo modo. $$ A = \{0, 1, 2, 3, ..., 98, 99\} $$ La sequenza inizia da 0 e termina a 99, inclusi tutti i numeri intermedi. Nota che l'elenco si ferma a 99, perché il numero 100 non soddisfa la condizione x<100.
Entrambi gli approcci sono validi e scelti in base al contesto e alla chiarezza richiesta. La notazione formale è più compatta e preferibile in contesti matematici formali e per insiemi molto grandi, mentre l'enumerazione può essere più immediata e visivamente accessibile per dimostrare esempi o insegnare concetti di base.
Gli insiemi numerici
In matematica è comune usare simboli specifici per rappresentare insiemi numerici standard, in modo che sia immediatamente chiaro a quale tipo di numeri ci si riferisce. Qui di seguito sono dettagliati i simboli dei principali insiemi numerici:
- \( \mathbb{N} \) per indicare l'insieme di tutti i numeri naturali. Questo insieme include tutti i numeri interi non negativi a partire da 0 o 1, a seconda della convenzione adottata (0, 1, 2, 3, ...). In alcuni contesti, \( \mathbb{N} \) inizia da 1 escludendo lo 0.
- \( \mathbb{Z} \) per indicare l'insieme di tutti i numeri interi. Questo insieme comprende tutti i numeri interi positivi e negativi, nonché lo zero (..., -3, -2, -1, 0, 1, 2, 3, ...).
- \( \mathbb{Q} \) per indicare l'insieme di tutti i numeri razionali. Un numero razionale è qualsiasi numero che può essere espresso come il quoziente o la frazione \( \frac{p}{q} \) di due interi, con il denominatore \( q \) diverso da zero (per esempio, \( \frac{1}{2} \), \( \frac{3}{4} \), \( -\frac{5}{3} \), ecc.).
- \( \mathbb{R} \) per indicare l'insieme di tutti i numeri reali. Questo insieme include tutti i numeri razionali \( \mathbb{Q} \), più tutti i numeri irrazionali (come \( \sqrt{2} \), \( \pi \), \( e \), ecc.), che non possono essere espressi come frazioni di interi.
- \( \mathbb{C} \) indica l'insieme dei numeri complessi, ossia tutti i numeri che possono essere espressi nella forma \( a + bi \), dove \( a \) e \( b \) sono numeri reali e \( i \) è l'unità immaginaria, tale per cui \( i^2 = -1 \). Questo insieme estende il campo dei numeri reali \( \mathbb{R} \) per includere soluzioni di equazioni che non hanno soluzioni reali, come \( x^2 + 1 = 0 \). Ad esempio nel numero complesso \( 3 + 4i \), il numero \( 3 \) rappresenta la parte reale e \( 4i \) la parte immaginaria del numero complesso.
Esempio. Supponiamo di voler illustrare come questi insiemi si intersecano e si sovrappongono. Possiamo immaginare un diagramma a cerchi concentrici, dove \( \mathbb{N} \) è il cerchio più interno, seguito da \( \mathbb{Z} \) che lo circonda completamente, indicando che tutti i numeri naturali sono anche interi. Poi abbiamo \( \mathbb{Q} \), che circonda \( \mathbb{Z} \), poiché ogni numero intero è anche razionale. Infine, \( \mathbb{R} \) è il cerchio esterno che contiene tutti gli altri, rappresentando l'insieme completo dei numeri reali, che comprende razionali e irrazionali. Questa rappresentazione aiuta a visualizzare come i diversi insiemi numerici si relazionano tra loro.
Le tipologie di insieme
Sulla base del numero degli elementi un insieme può essere definito.
- Insieme finito. L'insieme finito è composto da un numero definito di elementi. Ad esempio, l'insieme dei mesi in un anno e l'insieme dei giorni in un mese.
- Insieme infinito. L'insieme infinito è composto da un numero infinito di elementi. Ad esempio, l'insieme dei numeri naturali e l'insieme dei numeri reali.
- Insieme vuoto. L'insieme vuoto è un insieme privo di elementi. L'insieme vuoto è rappresentato con il simbolo Ø. Un esempio di insieme vuoto è l'insieme dei quadrati con tre lati.
- Insieme universo. L'insieme universo è l'insieme a cui appartengono tutti gli elementi degli altri insiemi. L'insieme universo è unico ed è generalmente indicato con la lettera maiuscola U. Tutti gli insiemi sono sottoinsiemi dell'insieme universo.
- L'insieme è un concetto primitivo e intuitivo. L'insieme è considerato come un concetto primitivo e intuitivo della matematica da molti studiosi. È un concetto primitivo in quanto è una nozione non derivata da concetti più elementari. È un concetto intuitivo in quanto è rappresentabile utilizzando un concetto molto simile a quello di un contenitore materiale degli oggetti Ciò vale, in particolar modo, per l'insieme finito di elementi. È quindi un concetto facilmente comprensibile da tutti.
- Differenza tra lista e insieme. Un insieme è composto da elementi differenti tra loro. Ad esempio, l'insieme A è composto dagli elementi { a, b, c }. Gli eventuali elementi uguali ripetuti in un insieme sono considerati come un unico elemento. Una lista, invece, è un contenitore composto anche da elementi ripetuti. Ad esempio, la lista L è composta dagli elementi { a, a, b, c, c }. Nel caso della lista gli elementi uguali ma ripetuti sono considerati come elementi a se stanti.
