Insieme complementare
L'insieme complementare ( insieme complemento ) è l'insieme degli elementi che non appartengono anche a un insieme di riferimento. Dati due insiemi A e B, in cui B è sottoinsieme di A, l'insieme complementare di B rispetto ad A è l'insieme differenza A - B ( differenza insiemi ).
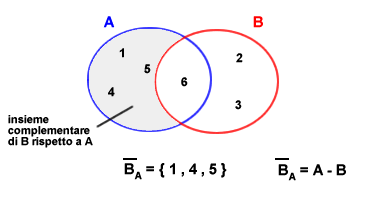
In tale caso si parla di insieme complementare relativo ( insieme differenza ) poiché il complemento di B è anch'esso un sottoinsieme delimitato dall'insieme A. Per comprendere meglio il concetto è possibile fare alcuni esempi pratici.
- L'insieme complementare relativo di un insieme vuoto Ø rispetto all'insieme A è uguale all'insieme A poiché A - Ø = A.
- L'insieme complementare relativo di un insieme A rispetto a se stesso è uguale a un insieme vuoto poiché A - A = Ø.
 Insieme complementare assoluto. Si parla, invece, di insieme complementare assoluto quando il complemento è un sottoinsieme dell'insieme universo. L'insieme universo è l'insieme più ampio a cui appartengono entrambi gli insiemi A e B. Nella seguente rappresentazione è raffigurato il caso dell'insieme complementare assoluto di B.
Insieme complementare assoluto. Si parla, invece, di insieme complementare assoluto quando il complemento è un sottoinsieme dell'insieme universo. L'insieme universo è l'insieme più ampio a cui appartengono entrambi gli insiemi A e B. Nella seguente rappresentazione è raffigurato il caso dell'insieme complementare assoluto di B.
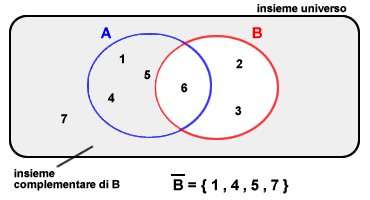
Nell'esempio precedente sono rappresentati un insieme A = { 1, 4, 5, 6 } e l'insieme B = { 2, 3, 6 }, entrambi contenuti in un medesimo insieme universo. Un elemento { 7 } non è compreso né in A e né in B. Il complementare assoluto di B comprende tutti gli elementi dell'insieme universo non appartenenti anche a B ossia { 1, 4, 5, 7 }. Viceversa, il complementare relativo di B rispetto ad A non prende in considerazione l'elemento { 7 } perché si trova al di fuori dell'insieme A.
