Unione insiemi
L'unione degli insiemi A e B è l'insieme degli elementi che appartengono all'insieme A oppure all'insieme B. In tale caso si afferma che "A è unito a B" e si scrive A ∪ B.
A ∪ B = { x | x ∈ A ∨ x ∈ B }
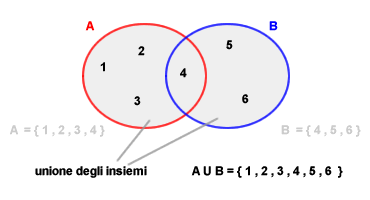
L'unione è rappresentata graficamente tramite l'intera area degli insiemi. Ad esempio, dato un insieme A ( cerchio rosso ) e un insieme B ( cerchio blu ), l'unione degli insiemi A e B è un insieme composto dagli elementi { 1, 2, 3, 4, 5, 6 } che appartengono all'insieme A { 1, 2, 3, 4 } oppure all'insieme B { 4, 5, 6 }. La rappresentazione grafica dell'unione degli insiemi è la seguente:
L'unione è una delle operazioni fondamentali della teoria degli insiemi. Può riguardare due o più insiemi. Dalla definizione emerge chiaramente che l'unione è una operazione commutativa:
A ∪ B = B ∪ A
L'unione degli insiemi è anche un'operazione associativa. Dati tre insiemi, la loro unione può essere scritta nel seguente modo indifferentemente:
( A ∪ B ) ∪ C = A ∪ ( B ∪ C )
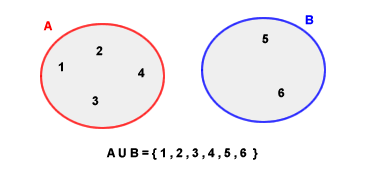
L'unione degli insiemi può essere effettuata anche se i due insiemi sono disgiunti ossia se non hanno elementi in comune ( intersezione vuota ). Un esempio di unione di insiemi disgiunti è il seguente.
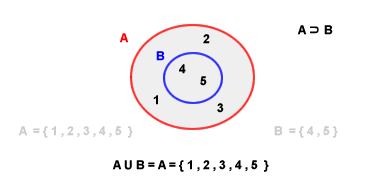
Se uno dei due insiemi è sottoinsieme dell'altro, l'unione dei due insiemi restituisce come risultato l'insieme più grande. Ad esempio, dati due insiemi A e B tale che B ⊂ A, allora A ∪ B = A.
L'operazione di unione utilizzata nell'insiemistica corrisponde all'operatore OR dell'algebra booleana e alla disgiunzione nella logica.

Proprietà dell'unione degli insiemi. L'operazione di unione tra insiemi gode di alcune proprietà simili a quelle della moltiplicazione e dell'addizione dei numeri naturali. In particolar modo, l'intersezione gode della proprietà commutativa, associativa e distributiva rispetto all'intersezione.
