Partizione insieme

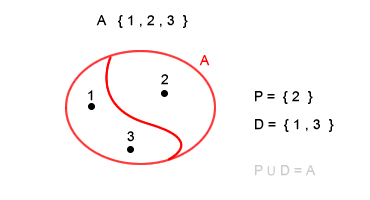
La partizione di un insieme è l'insieme dei suoi sottoinsiemi non vuoti e disgiunti tra loro, la cui unione sia sempre uguale all'insieme di origine. La partizione di un insieme A è la divisione di A in più sottoinsiemi, dette parti ( blocchi o classi ) della partizione. I sottoinsiemi della partizione coprono interamente l'insieme di origine senza mai sovrapporsi fra loro. Ad esempio, dato un insieme A composto dagli elementi { 1, 2, 3 } possiamo suddividere l'insieme in un sottoinsieme P di numeri pari { 2 } e in un sottoinsieme D di numeri dispari { 1, 3 }. I due sottoinsiemi non sono vuoti e non si sovrappongono. L'unione dei due sottoinsiemi P U D restituisce come risultato finale l'insieme di origine A. Possiamo quindi affermare che l'insieme { P , D } è una partizione dell'insieme A.

Condizioni di una partizione. La partizione di A è una collezione di sottoinsiemi dell'insieme A che soddisfa le seguenti condizioni:

• Tutti i sottoinsiemi della partizione non sono vuoti.
• Tutti i sottoinsiemi della partizione sono disgiunti fra loro.
• L'unione di tutti i sottoinsiemi della partizione è uguale all'insieme A.

Quando una partizione è composta da soli due insiemi, come nell'esempio precedente, si dice bipartizione. Quando la partizione è composta da tre sottoinsiemi si dice tripartizione. Più in generale, una partizione composta da k sottoinsiemi si dice k-partizione.