Intersezione insiemi
L'intersezione di due insiemi A e B è l'insieme degli elementi che appartengono sia all'insieme A e sia all'insieme B. In tale caso si afferma che "A è intersecato con B" e si scrive A ⋂ B.
A ⋂ B = { x | x ∈ A e x ∈ B }
L'intersezione è una delle operazioni fondamentali degli insiemi. Nella rappresentazione grafica l'intersezione di due insiemi è individuata dall'area in comune tra i due cerchi ( insiemi ). L'area in comune tra il cerchio rosso ( insieme A ) e il cerchio blu ( insieme B ) è caratterizzato dagli stessi elementi { 1 , 2 } che appartengono sia all'insieme A che all'insieme B. Si tratta pertanto di una intersezione tra i due insiemi.
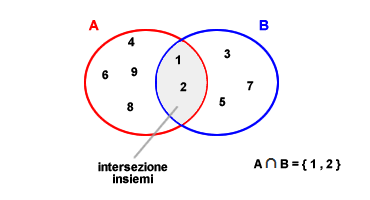
Come si può notare facilmente nella rappresentazione grafica, l'area di intersezione è un sottoinsieme proprio di entrambi gli insiemi. Possiamo quindi scrivere nel seguente modo:
A ⋂ B ⊂ B
A ⋂ B ⊂ A
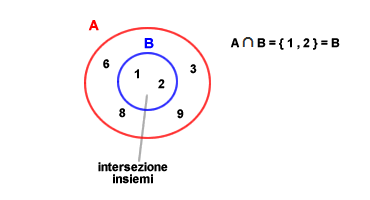
In alcuni casi particolari l'intersezione coincide con il sottoinsieme improprio di uno dei due insiemi. Ciò accade quando tutti gli elementi di un insieme sono contenuti nell'area di intersezione. Nel seguente caso la zona di intersezione coincide con l'insieme B ( cerchio blu ). In questo caso l'area di intersezione A ⋂ B è un sottoinsieme proprio dell'insieme A e un sottoinsieme improprio dell'insieme B.
Proprietà intersezione insiemi. L'operazione di intersezione tra insiemi gode di alcune proprietà simili a quelle della moltiplicazione e dell'addizione dei numeri naturali. In particolar modo, l'intersezione gode della proprietà commutativa, associativa e distributiva rispetto all'unione.
Insiemi disgiunti. Quando due insiemi non hanno elementi in comune, ossia quando non esiste alcuna intersezione, gli insiemi sono detti insiemi disgiunti. Dal punto di vista grafico gli insiemi disgiunti non hanno nessuna area in comune.
