Estremo superiore di un insieme
L'estremo superiore di un insieme non vuoto A è il più piccolo numero reale che è maggiore o uguale a ogni elemento di A.
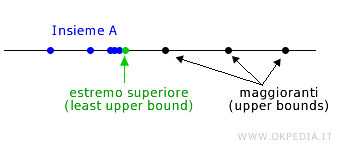
E' anche detto limite minimo superiore (least upper bound) o supremo (supremum).
Questo numero, che può appartenere a A oppure no, serve a delimitare superiormente A ed è indicato con il simbolo sup(A).
$$ \sup(A) $$
La definizione di estremo superiore
Formalmente, per un insieme non vuoto A di numeri reali, un numero x è il supremo di A se soddisfa due condizioni:
- x è un maggiorante di A, ovvero x è maggiore o uguale a ogni altro elemento dell'insieme A $$ \forall \ a \in A \Rightarrow a \leq x $$
- x è il minimo tra i maggioranti di A, cioè x è minore o uguale a ogni altro maggiorante y di A $$ \forall \ y \in R \ , \ (\forall \ a \ \in A, a \leq y) \Rightarrow \sup(A) \leq y $$
Se l'estremo superiore di A è anche un elemento dell'insieme A, allora è detto il massimo di A e si indica con max(A). $$ \sup(A) \in A \Rightarrow \sup(A) = \max(A) $$
Esempi
Esempio 1
Per l'insieme finito A, tutti gli elementi sono minori o uguali a 5, quindi 5 è un maggiorante di A.
$$ A = \{1, 2, 3, 4\} $$
Tuttavia, 4 è il minimo dei maggioranti e quindi il supremo di A.
$$ \sup(A) = 4 $$
In questo caso, il supremo coincide con il massimo di A.
$$ \sup(A) = \max(A) = 4 $$
Esempio 2
L'insieme dei numeri naturali è illimitato superiormente,
$$ N = \{1, 2, 3, 4, 5, \ldots \} $$
Il suo estremo superiore è l'infinito positivo (∞) perché non esiste un numero reale superiore a qualsiasi numero naturale.
$$ \sup(N) = +\infty $$
In questo insieme l'estremo superiore non appartiene all'insieme N.
Pertanto, l'insieme N ha un estremo superiore ma non ha un massimo.
