insiemi disgiunti

Gli insiemi disgiunti sono due insiemi senza elementi in comune. Dati due insiemi A e B, si dicono disgiunti quando nessun elemento dell'insieme A appartiene anche all'insieme B e viceversa. La rappresentazione grafica degli insiemi disgiunti è la seguente:

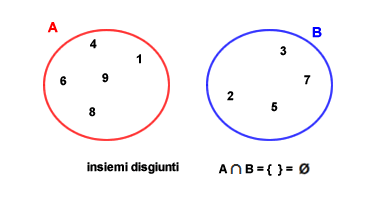
Nel caso degli insiemi disgiunti non esiste alcun'area di intersezione tra i due insiemi. Il risultato dell'operazione di intersezione tra A e B, essendo un insieme privo di elementi, è coincidente con l'insieme vuoto Ø.

Nell'esempio precedente, gli insiemi A e B sono composti da un numero finito di elementi. L'insieme A è formato dagli elementi { 1, 4, 6, 8, 9 } e l'insieme B dagli elementi { 2, 3, 5, 7 }. Come si può notare, i due insiemi non hanno nessun elemento in comune e, pertanto, sono insiemi disgiunti.

Anche gli insiemi infiniti possono essere disgiunti. Ad esempio, l'insieme dei numeri naturali pari ( P ) e dei numeri naturali dispari ( D ) hanno infiniti elementi ma nessun elemento in comune e, pertanto, sono insiemi disgiunti.