Sottoinsieme improprio
Dati due insiemi A e B, l'insieme A è un sottoinsieme improprio di B se tutti gli elementi dell'insieme A appartengono anche a B e tutti gli elementi di B appartengono anche a A.
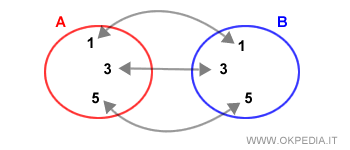
Ogni insieme non vuoto ha sempre due sottoinsiemi impropri: l'insieme stesso e l'insieme vuoto.
L'insieme stesso
Qualsiasi insieme non vuoto è sempre un sottoinsieme di se stesso.
Dimostrazione
L'insieme A è sottoinsieme di se stesso perché è sempre vero che A ⊆ A.
A ⊆ A
Qualsiasi insieme non vuoto è incluso in un insieme uguale.
E' quindi un sottoinsieme improprio dell'insieme stesso.
Esempio
Un esempio di sottoinsieme improprio di se stesso è il seguente:
{ 1, 2, 3, 4, 5 } ⊆ { 1, 2, 3, 4, 5 }
L'insieme è incluso nell'insieme stesso.
L'insieme vuoto
Dato un qualsiasi insieme A non vuoto e un insieme vuoto ø, è possibile sempre affermare che l'insieme vuoto è incluso nell'insieme A.
ø ⊆ A
Quindi l'insieme vuoto ø è un sottoinsieme improprio, perché è un sottoinsieme di qualsiasi insieme non vuoto.
Nota. Questa affermazione deriva dal fatto che l'insieme vuoto non ha elementi. Pertanto, ogni elemento dell'insieme vuoto ( non elemento ) è da considerarsi anche un elemento per qualsiasi altro insieme.
Dimostrazione
Partamo dall'ipotesi:
ø ⊆ A
Se questa ipotesi non fosse vera, dovremmo essere in grado di trovare almeno un elemento dell'insieme vuoto ø che non appartiene all'insieme A.
Tuttavia, non è possibile trovare alcun elemento dell'insieme vuoto, perché l'insieme vuoto non ha elementi.
{ } ⊆ { 1, 2, 3, 4, 5 }
Quindi l'ipotesi ø ⊆ A non può essere falsa.
Essendo impossibile che sia falsa, allora l'ipotesi ø ⊆ A è vera.
Per questo motivo l'insieme vuoto ø è considerato un sottoinsieme improprio dell'insieme A e, più in generale, di qualsiasi altro insieme non vuoto.
Nota. Si tratta di una dimostrazione per assurdo perché parte dall'ipotesi opposta per dimostrare la sua impossibilità.
