Doppia implicazione ( equivalenza logica )
La doppia implicazione è connettivo logico dell'algebra booleana. Date due proposizioni logiche A e B, la doppia implicazione determina una terza proposizione A ⇔ B che si presenta vera soltanto se entrambe le proposizioni A e B sono vere o se entrambe le proposizioni A e B sono false. La doppia implicazione tra A e B equivale a dire che "A implica B" ( A⇒B ) e "B implica A" ( A⇐B ). La doppia implicazione viene indicata con la doppia freccia A ⇔ B interposta tra le due proposizioni logiche e si legge "A se e solo se B". La doppia implicazione esprime una relazione bicondizionale ed è conosciuta anche come equivalenza ( o equivalenza logica ). La tabella di verità della doppia implicazione è la seguente.
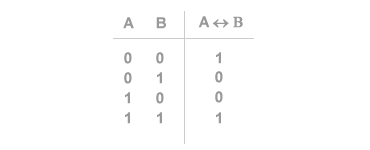
La doppia implicazione è utilizzata per esprimere la condizione necessaria e sufficiente tra due proposizioni logiche ( variabili logiche ). Quando scriviamo A ⇔ B possiamo dire che A è una condizione necessaria e sufficiente per B e viceversa.
Esempio di doppia implicazione. Un triangolo è equilatero ( A ) se e solo se il triangolo possiede tre angoli uguali ( B ). Se la proposizione A è vera, allora anche la proposizione B è vera, e viceversa.
Equivalenza logica. Nella logica proposizionale l'equivalenza logica è indicata con il simbolo ≡. Date due formule A e B, queste sono logicamente equivalenti quando sono entrambe vere nello stesso insieme di modelli. In altri termini, A e B sono logicamente equivalenti quando A è conseguenza logica di B e B è conseguenza logica di A.
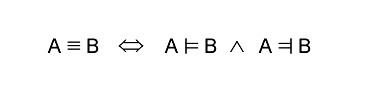
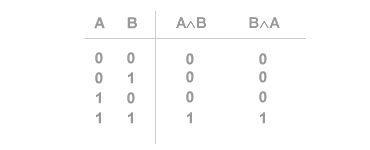
Ad esempio la formula ( A ∧ B ) è equivalente alla formula ( B ∧ A ) poiché quando è vera la prima è necessariamente vera anche la seconda, e viceversa ( regola di commutatività del connettivo logico AND ).
Allo stesso modo la formula ( A ∨ B ) è equivalente alla formula ( B ∨ A ) poiché quando è vera la prima è necessariamente vera anche la seconda, e viceversa ( regola di commutatività del connettivo logico OR ). Le equivalenze logiche nella logica proposizionale non si esauriscono alle semplici regole di commutatività delle formule. Ad esempio, altri esempi di equivalenze logiche sono le leggi di De Morgan.
