Modus tollens

Il modus tollens è una regola logica d'inferenza e una forma di ragionamento. Date due proposizioni logiche A e B e una implicazione A→B ( A implica B ), se la proposizione A→B è vera e la proposizione B ( conseguente ) è falsa, allora anche la proposizione A ( antecedente ) è falsa. Il modus tollens deriva dal latino e può essere tradotta letteralmente nel modo che toglie la verità di una proposizione, togliendo anche la verità dell'altra proposizione. La tabella di verità del modus tollens è la seguente.

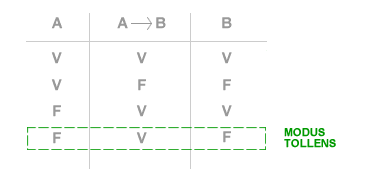
In base alla notazione dei connettivi logici il modus tollens può essere rappresentato nella seguente forma:

La notazione logica si legge "dall'implicazione (A→B) vera e dalla proposizione B falsa, allora anche la proposizione A è falsa". La regola logica del modus tollens può essere rappresentata anche nella seguente forma:

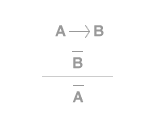
Il modus tollens è un caso di sillogismo ipotetico in cui la seconda premessa è una proposizione accolta sulla base di un'evidenza empirica, ossia non è ottenuta da un processo deduttivo bensì da uno stato di fatto.

Esempio di modus tollens. Date due proposizioni logiche ( A e B ) e una implicazione ( A→B ), la proposizione logica A afferma "Piove". La proposizione logica B afferma "La strada è bagnata". La proposizione di implicazione materiale afferma A→B afferma "se piove, allora la strada è bagnata". Se la proposizione B è falsa ( "la strada non è bagnata" ) e l'implicazione A→B è vera, allora anche la proposizione A è falsa ( "non piove" ).