Modus ponens
Il modus ponens è una regola logica d'inferenza alla base del ragionamento logico e della deduzione. Date due proposizioni logiche A e B e una implicazione A→B ( A implica B ), se la proposizione A→B è vera e la proposizione A ( premessa ) è vera, allora anche la proposizione B ( conseguenza o conclusione ) è vera. Il modus ponens deriva dal latino modus ponendo ponens che può essere tradotta letteralmente come "modo che afferma". La tabella di verità del modus ponens è la seguente:
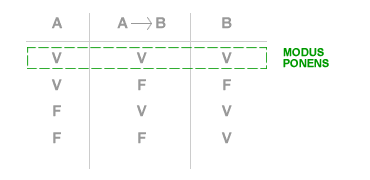
Secondo la notazione degli operatori logici il modus ponens può essere scritto nel seguente modo:
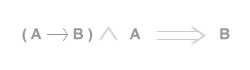
La notazione logica si legge "dall'implicazione (A→B) vera e dalla proposizione A vera, si deduce logicamente che anche la proposizione B è vera". La congiunzione tra le proposizioni-premessa ( A→B ) e A, conduce alla deduzione della proposizione-conclusione B. La regola del modus ponens può essere rappresentata anche nella seguente forma:
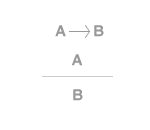
Il modus ponens è una forma di deduzione ( metodo deduttivo ). A partire da due premesse vere, il metodo del modus ponens consente di dedurre logicamente una conclusione ( conseguenza ) anch'essa vera. Le due premesse sono due proposizioni logiche, una proposizione logica consiste in un'asserzione condizionale ( se-allora ) mentre la seconda proposizione in un'ipotesi di asserzione condizionale. Il modus ponens è anche detto ragionamento diretto, principio di disgiunzione o affermazione dell'antecedente. Quando una regola di inferenza si basa sul modus ponens, viene detta inferenza deduttiva. Quando le premesse sono vere e la conclusione è vera, si parla di inferenza fondata. Laddove una o più premesse sono false ( F) si parla, invece, di inferenza infondata. Il modus ponens ci dice soltanto che la conclusione è vera ( V ) se tutte le premesse sono vere ( V ).
Esempio di modus ponens. Per comprendere il modus ponens è consigliabile ricorrere a un esempio. Prendiamo come esempio due proposizioni logiche e una implicazione. La proposizione logica A afferma "Piove". La proposizione logica B afferma "La strada è bagnata". La proposizione di implicazione materiale afferma A→B afferma "se piove, allora la strada è bagnata". Se la proposizione A è vera ( "piove" ) e l'implicazione A→B è vera, allora anche la proposizione B è vera ( "la strada è bagnata" ). In questo esempio l'inferenza deduttiva è fondata poiché entrambe le premesse sono vere e anche la conclusione è vera.
Differenza tra i simboli di implicazione e ragionamento deduttivo. È opportuno sottolineare la differenza tra il simbolo → e il simbolo ⇒. Il simbolo → rappresenta il connettivo logico dell'implicazione materiale tra le proposizioni logiche A e B. Il simbolo ⇒ rappresenta, invece, il ragionamento deduttivo.
