Equilibrio di Nash

L'equilibrio di Nash è una combinazione di strategie in cui ciascun giocatore effettua la migliore scelta possibile ( strategia dominante ) sulla base dalle aspettative di scelta dell'altro giocatore. L'equilibrio di Nash è la combinazione di mosse ( m₁, m₂ ) in cui la mossa di ciascun giocatore è la migliore risposta alla mossa effettuata dall'altro giocatore. Ogni giocatore formula delle aspettative sulla scelta dell'altro e, in base a queste, decide la propria strategia ( "fare il meglio per sé e per gli altri" ). Un equilibrio di Nash è un equilibrio stabile, poiché nessun giocatore ha interesse a modificare la propria decisione ( strategia ). Ogni giocatore trae l'utilità massima possibile dalle proprie scelte, tenendo conto della migliore scelta dell'altro giocatore. Qualsiasi variazione strategica potrebbe soltanto peggiorare la sua posizione ( payoff / utilità ). L'equilibrio di Nash rappresenta una situazione di equilibrio ottimale di un gioco non cooperativo e, per questa ragione, è anche conosciuto come equilibrio non cooperativo. L'equilibrio di Nash non deriva da un accordo tra le parti ( giocatori ), bensì dall'adozione di strategie dominanti da parte di tutti i giocatori, tali da garantire sia il migliore risultato possibile per ciascun giocatore ( ottimo individuale ) che il migliore equilibrio collettivo ( ottimo sociale ). Nella seguente matrice payoff è rappresentato un esempio di equilibrio di Nash in un gioco non cooperativo a due giocatori. Per motivi di semplicità l'esempio si basa su due giocatori, l'equilibrio di Nash può comunque essere esteso anche a N giocatori.

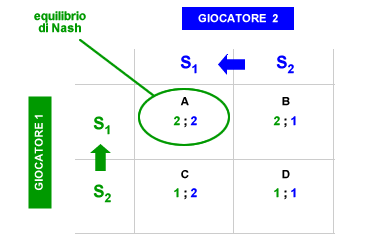
Nella matrice ogni giocatore può scegliere la strategia S₁ o la strategia S₂. Il giocatore S₁ si aspetta che il giocatore 2 scelga S₁ ( strategia dominante ) e, quindi, adotta anch'egli la strategia S₁ in quanto gli consente di ottenere un pay-off individuale pari a 2. Anche per il giocatore 2 formula delle aspettative sulle scelte dell'avversario e si attende che il giocatore 1 scelga S₁, scegliendo a sua volta la strategia S₁. L'equilibrio del gioco converge verso la cella A della matrice ( in alto a sinistra ) dove entrambi i giocatori massimizzano il proprio pay-off individuale ( ottimo individuale ) dopo aver scelto la propria strategia dominante ( equilibrio di Nash ). Entrambi i giocatori hanno formulato un'ipotesi sulla migliore scelta ( strategia dominante ) del giocatore avversario e, sulla base di questa, hanno scelto la propria strategia dominante. Il seguente esempio consente di capire meglio il processo decisionale alla base dell'equilibrio di Nash.

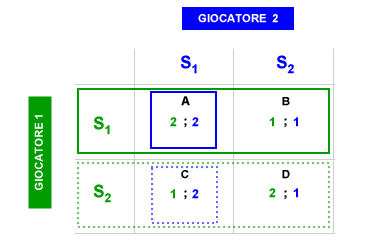
Il giocatore 1 ( verde ) potrebbe scegliere sia S₁ che S₂, in entrambi i casi può sperare di ottenere per sé il pay-off più alto ( 2 ) nelle celle A e D. Il giocatore 1 ( verde ) però sa bene che se scegliesse S₂, il giocatore 2 ( blu ) sceglierebbe poi S₁ e l'equilibrio finale si collocherebbe nella cella C, dove il giocatore 1 ottiene il pay-off più basso ( 1 ). Scegliendo S₁, invece, il giocatore 1 ( verde ) è consapevole che anche il giocatore 2 ( blu ) avrebbe la convenienza a scegliere S₁ e l'equilibrio finale si collocherebbe nella cella A, dove il giocatore 1 ottiene il pay-off più alto ( 2 ). Seguendo un ragionamento simile, quando spetta al giocatore 2 ( blu ) scegliere per primo, questi è consapevole che scegliendo S₁ anche il giocatore 1 ( verde ) avrebbe la convenienza a scegliere S₁. Anche in questo caso l'equilibrio strategico si colloca nella cella A. La cella A è un equilibrio di Nash. Tutte le altre celle, invece, non lo sono. L'equilibrio di Nash è sintetizzabile con la seguente frase: "Vincere facendo il meglio per sé e per gli altri". L'equilibrio di Nash è un concetto teorico fondamentale della teoria dei giochi e dell'economia politica.

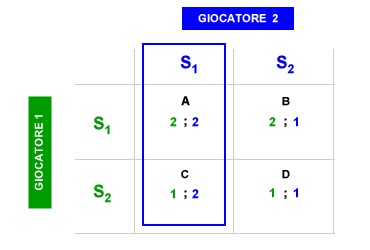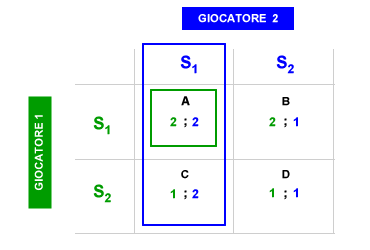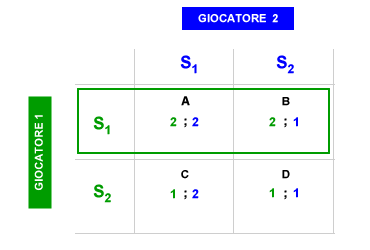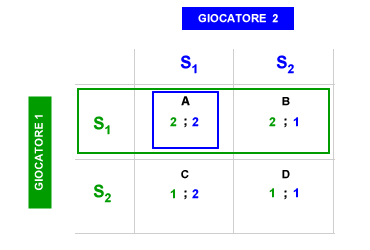
Ottimo sociale. Nell'equilibrio di Nash può verificarsi una situazione ottimale per entrambi i giocatori e una situazione ottimale per l'intera collettività. Ad esempio, quando il giocatore 1 ( verde ) sceglie S₁ per primo, il giocatore 2 ( blu ) risponde scegliendo S₁ e l'equilibrio si posiziona nella cella A. Quando il giocatore 2 ( blu )sceglie per primo S₁, il giocatore 1 ( verde ) sceglie S1 e l'equilibrio si posiziona nuovamente nella cella A. La cella A è, quindi, un equilibrio di Nash. Nella cella A entrambi i giocatori ottengono un pay-off pari a 2 ( ottimo individuale ) e la somma dei pay-off individuali 2+2 è uguale a 4 ( ottimo sociale ). In conclusione, nella cella A ( equilibrio di Nash ) si verifica sia una situazione di ottimo individuale per ogni giocatore che una situazione di ottimo sociale per l'intera collettività.

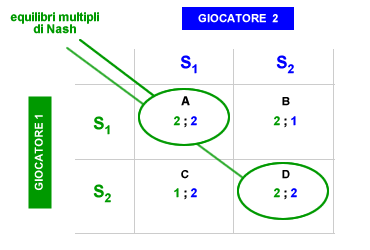
Equilibri multipli di Nash. Un gioco non cooperativo può presentare più equilibri di Nash. Anche in presenza di equilibri multipli, ogni equilibrio di Nash del gioco è comunque un equilibrio stabile, poiché dalla sua posizione ( equilibrio locale ) qualsiasi scelta è peggiorativa per ogni giocatore. Ad esempio, nella seguente matrice pay-off sono presenti due equilibri di Nash simmetrici.

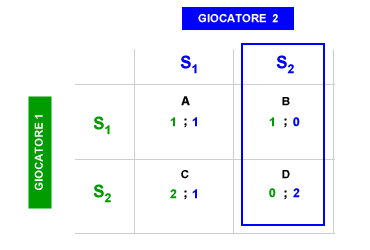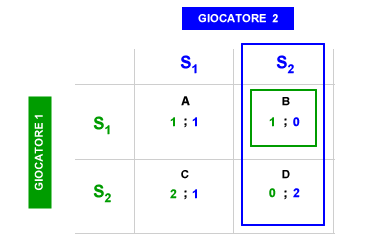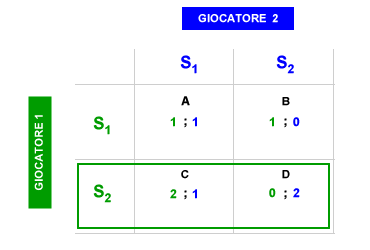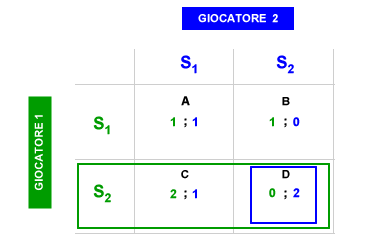
Assenza equilibrio di Nash. Un altro problema dell'equilibrio di Nash è la possibilità che manchino del tutto le condizioni per determinarlo. Molti giochi sono privi di equilibrio di Nash. Ad esempio, nel seguente caso è assente l'equilibrio di Nash. Quando il giocatore 1 sceglie S₂, il giocatore 2 sceglie S₂ e l'equilibrio si posiziona sulla casella D. Viceversa, quando il giocatore 2 sceglie S₂, il giocatore 1 sceglie S₁ e l'equilibrio si posiziona sulla casella B. Nel seguente gioco, quindi, non esiste l'equilibrio di Nash.

Dilemma del prigioniero. L'adozione delle strategie dominanti non assicura sempre un equilibrio di ottimo sociale. In assenza di informazioni, il gioco non cooperativo potrebbe convergere verso un equilibrio stabile ma non anche ottimale. L'ipotesi è dimostrata nel problema del "dilemma del prigioniero" in cui due operatori, pur formulando delle aspettative razionali sul comportamento dell'avversario e adottando strategie dominanti, determinano un equilibrio sub-ottimale ( D ) sia dal punto individuale che sociale. L'equilibrio D è un equilibrio di Nash ma non anche una situazione di ottimo paretiano. In conclusione, l'equilibrio di Nash e l'ottimo di Pareto sono due situazioni economiche diverse, poiché sono determinate da condizioni differenti.

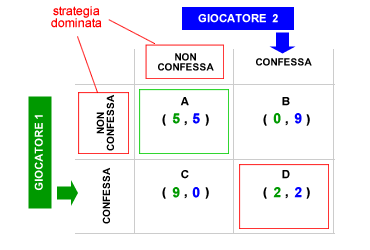
Ad esempio, il giocatore 1 si aspetta che il giocatore 2 confessi, poiché la strategia dominante del giocatore 2 è confessare. Grazie alla confessione il giocatore 2 otterrebbe la libertà ( pay-off 9). Sulla base di questa aspettativa, il giocatore sceglie la strategia dominante tra B e D, scegliendo a sua volta di confessare per ottenere un pay-off almeno pari a 2. Lo stesso ragionamento viene adottato, in modo inverso, dal giocatore 2. L'equilibrio D è un equilibrio di Nash ed è un equilibrio stabile poiché nessuno dei due giocatori ha interesse a modificare le proprie scelte. L'equilibrio D non è, però, un ottimo paretiano in quanto i due giocatori ottengono un pay-off sub-ottimale ( 2 ) rispetto a quello che avrebbero ( 5 ) se decidessero di non confessare ( equilibrio A ).

Equilibrio di Cournot. L'equilibrio di Nash è un concetto teorico di equilibrio simile all'equilibrio di Cournot. Nel duopolio di Cournot ogni impresa sceglie il livello di produzione ottimale sulla base della decisione strategica dell'altra impresa concorrente.

---

• La soluzione del gioco è un equilibrio di Nash. Quando un gioco ha un'unica soluzione razionale, individuabile tramite la teoria dei giochi, tale soluzione è anche un equilibrio di Nash. Tuttavia, non è detto che un equilibrio di Nash sia anche la soluzione ottimale del gioco o l'unica soluzione del gioco, in quanto possono esistere diversi equilibri di Nash in un gioco. In conclusione, un equilibrio di Nash non è detto che sia anche un ottimo paretiano.
• Equilibrio di Nash in un gioco sequenziale. In un gioco sequenziale l'equilibrio di Nash è la combinazione di mosse dei giocatori, in cui ogni mossa di ciascun giocatore è sempre la migliore risposta alla mossa dell'altro. L'eliminazione iterata delle strategie dominate conduce verso un equilibrio di Nash.
• Critica alla mano invisibile di Adam Smith. L'equilibrio di Nash è una critica alla teoria della "mano invisibile" di Adam Smith. Secondo Adam Smith, la tendenza di ogni agente economico a massimizzare il proprio benessere ( utilità ) porta l'equilibrio del mercato verso una situazione ottimale per tutti ( ottimo paretiano ). Viceversa, Nash dimostra che ciò non è sempre detto. La selezione della scelta migliore per ciascuno ( strategia dominante ) può condurre anche verso equilibri sub-ottimali, sia dal punto di vista privato/individuale che dal punto di vista sociale.
• Equilibrio di Nash e ottimo paretiano. Un altro esempio di equilibrio di Nash non ottimale si verifica nel pubblico durante uno spettacolo. Tutti gli spettatori potrebbero vedere lo spettacolo seduti. Tuttavia, se uno di essi si alzasse vedrebbe meglio degli altri ( ottimo individuale ). Aspettandosi che gli altri si alzino per vedere meglio, tutti gli spettatori iniziano ad alzarsi. In conclusione, tutti gli spettatori assistono in piedi allo spettacolo, più scomodi e con una visione peggiore ( equilibrio sub-ottimale ) rispetto a quella che avrebbero restando seduti ( ottimo sociale ).