Dilemma del prigioniero

Il dilemma del prigioniero è una situazione in cui le scelte individuali dei giocatori, pur essendo strategie dominanti, determinano un equilibrio inefficiente. Nella teoria dei giochi ( game theory ) il dilemma del prigioniero dimostra l'inefficienza delle scelte individuali in particolari situazioni di gioco.

Ad esempio, dati due giocatori separati in stanze diverse, senza la possibilità di comunicare tra loro ( informazione imperfetta ), la seguente matrice pay-off evidenzia il tipico caso del dilemma del prigioniero. Due giocatori sono accusati di un reato e interrogati contemporaneamente. Nelle celle della matrice sono indicati i livelli di utilità individuale dei due giocatori in relazione alle diverse combinazioni di scelta possibili.

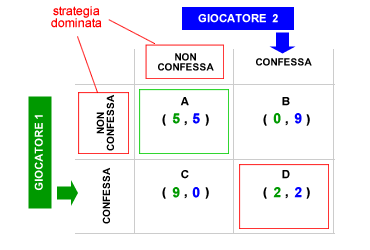
Il giocatore che confessa il reato accusando l'altro ottiene la scarcerazione immediata ( utilità 9 ) mentre il giocatore accusato subisce la massima pena ( utilità 0 ). Se entrambi i giocatori evitano di confessare, ai due viene applicata una pena molto lieve ( utilità 5 ). Viceversa, se entrambi confessano, entrambi sono condannati alla pena ordinaria ( utilità 2 ).

Entrambi i giocatori si attendono che l'altro confessi, poiché l'atto di "confessare" è la strategia dominante. Sulla base di questa aspettativa di scelta altrui, i giocatori decidono la propria strategia dominante e, a loro volta, decidono di confessare.

Al giocatore 1 converrebbe confessare, poiché ciò gli consente di ottenere un pay-off individuale più alto ( strategia dominante ) pari a 9. È quindi lecito e razionale che il giocatore 2 si attenda la confessione del giocatore 1 ( es."se non confesso io, confessa lui" ). Tenendo conto di questo aspetto, il giocatore 2 decide a sua volta di confessare. Lo stesso ragionamento viene effettuato dal giocatore 1.

Nel caso del dilemma del prigioniero, quindi, le strategie dominanti attese degli individui determinano un equilibrio non efficiente ( cella D ). Nel dilemma del prigioniero l'equilibrio del gioco non è né un ottimo individuale, né un ottimo sociale.

Per raggiungere l'ottimo sociale i due giocatori dovrebbero non confessare ( strategia dominata ). Nella cella A ( ottimo sociale ) il pay-off collettivo è pari a 10 in quanto entrambi i giocatori ottengono un pay-off individuale pari a 5. Pur essendo un risultato individuale sub-ottimale, la cella A è il migliore risultato possibile per entrambi i giocatori ( collettività ).

La spinta individuale a massimizzare l'utilità personale fino a 9 ( celle B e C ) e il timore che l'altro confessi, porta entrambi i giocatori verso il peggiore equilibrio sociale possibile e al peggioramento del pay-off individuale ( cella D ).

• Inefficienza individuale. Nella cella D entrambi i giocatori sono condannati e ottengono un pay-off individuale molto basso ( 2 ).
• Inefficienza sociale. Nella cella D si riscontra il peggiore risultato collettivo possibile. La somma dei pay-off individuali (2+2) è soltanto pari a 4 ed è inferiore a quella ottenibile nelle altre celle della matrice.

Informazione perfetta. Il dilemma del prigioniero potrebbe essere risolto fornendo ai due giocatori ( accusati ) la possibilità di comunicare tra loro. Così facendo, i due giocatori sarebbero in grado di controllare la decisione dell'altro.

Autorità centrale. Un altro modo per risolvere il dilemma del prigioniero è l'istituzione di un'autorità centrale, in grado di controllare e di imporre il rispetto dell'accordo tra le parti ( accordo vincolante ).

Concorrenza tra imprese. In ambito economico il dilemma del prigioniero è una situazione simile a quella di due o più imprese che tentano di aumentare la propria quota di mercato attraverso una riduzione dei prezzi. In assenza di un accordo vincolante, ogni impresa riduce i prezzi di vendita per aumentare la propria quota di mercato a scapito dell'altra. Così facendo, entrambe le imprese riducono i prezzi senza aumentare la propria quota di mercato e ciò potrebbe peggiorare la situazione economica di entrambe le imprese. Alle due imprese converrebbe stipulare un accordo vincolante, limitare la concorrenza e mantenere i prezzi alti.

Equilibrio di Nash. Il dilemma del prigioniero è la dimostrazione che le strategie dominanti non implicano sempre un equilibrio ottimale ( ottimo paretiano ). Secondo Nash, ogni giocatore sceglie la propria strategia dominante sulla base delle aspettative di scelta del giocatore avversario. Anche in questo caso, il dilemma del prigioniero dimostra come le strategie dominate non è detto che conducano sempre verso equilibri ottimali. Il giocatore 1 si aspetta che il giocatore confessa e, quindi, a sua volta confessa. Il giocatore 2 si aspetta che il giocatore 1 confessa e, a sua volta, confessa. Il risultato finale è un equilibrio stabile ( equilibrio di Nash ) ma sub-ottimale sia dal punto di vista individuale che sociale. In conclusione, l'equilibrio di Nash e l'ottimo paretiano corrispondono a due situazioni differenti e distinte tra loro.