Effetto orizzonte
L'effetto orizzonte è un problema degli algoritmi di ricerca in profondità con taglio di ricerca che si verifica nella teoria dei giochi. Un algoritmo di ricerca in profondità con taglio di ricerca analizza le decisioni migliori tenendo conto soltanto delle N mosse successive. Al raggiungimento della N-esima mossa interrompe la ricerca ( taglio di ricerca ). Questa tecnica consente di ridurre il tempo di elaborazione necessario per determinare una decisione. D'altra parte, la tecnica non possiede una visione lungimirante, al contrario è una tecnica "miope", poiché non può valutare le mosse successive a partire dalla N+1. Questo limite è detto "effetto orizzonte". L'effetto orizzonte porta l'algoritmo a decisioni che potrebbero rivelarsi sub-ottimali o addirittura perdenti in un orizzonte di gioco più ampio.
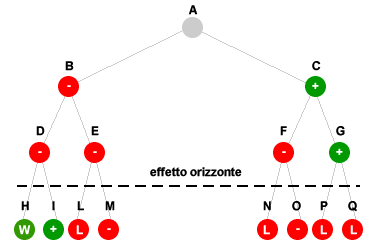
Esempio di effetto orizzonte. Nel precedente albero di gioco l'algoritmo deve intraprendere una decisione a partire dal nodo A, analizzando soltanto i nodi fino al 2° livello. I nodi verdi sono mosse positive, quelli rossi sono mosse sfavorevoli al giocatore. Il nodo verde "W" indica la vittoria della partita ( nodo terminale favorevole ) mentre il nodo rosso indica la sconfitta ( nodo terminale sfavorevole ). L'algoritmo non riesce a valutare i nodi al di sotto dell'orizzonte temporale ( H-Q). Sulla base di questo limite l'algoritmo individua come cammino ottimale il percorso A-C-G. Così facendo però l'algoritmo porta il gioco verso una sconfitta sicura per il giocatore in quanto i nodi successivi al nodo G sono entrambi nodi terminali sfavorevoli (sconfitta). L'algoritmo non può saperlo poiché si trovano entrambi oltre l'orizzonte di gioco. Allo stesso modo, l'algoritmo non riesce a individuare il nodo terminale favorevole H ( vittoria ) poiché anche questo si trova oltre la linea dell'orizzonte.
Soluzioni al problema dell'effetto orizzonte. Il problema dell'effetto orizzonte si verifica per la prima volta nei primi programmi per gli scacchi. Per rendere accessibile il tempo decisionale di calcolo del computer, gli algoritmi di gioco analizzano le varianti di gioco fino a una determinata profondità e selezionano le varianti migliori. Ad esempio, sei mosse a partire dalla situazione corrente di gioco. Tuttavia, queste scelte sono ottimali soltanto entro l'orizzonte di gioco considerato e non è detto che lo siano anche oltre. L'effetto orizzonte è una sorta di "miopia" dell'algoritmo di ricerca. L'algoritmo "non vede" la settima mossa, la quale potrebbe anche essere una sconfitta del computer per scatto matto. Le possibili soluzioni al problema dell'effetto orizzonte nel gioco degli scacchi sono le seguenti:
Aumento della profondità. Per ridurre il rischio dell'effetto orizzonte è necessario aumentare la profondità di analisi degli algoritmi di ricerca. Tuttavia, a parità di risorse hardware, ogni ulteriore aumento della profondità di analisi dell'albero di gioco comporta un aumento esponenziale del tempo di elaborazione, nonché della complessità spaziale e temporale di esecuzione.
Metodo selettivo. Un'altra soluzione al problema dell'effetto orizzonte consiste nella selezione delle mosse più promettenti tramite una funzione di valutazione, in modo da concentrare la ricerca in profondità soltanto su queste varianti di gioco. I criteri di selezione consentono di eliminare dalla ricerca tutte quelle varianti iniziali poco interessanti per concentrarsi su quelle più interessanti. L'efficacia del metodo selettivo è fortemente collegata all'efficacia della funzione di valutazione empirica.
Database dei finali. I moderni programmi di scacchi utilizzano dei database precalcolati con tutte le possibili mosse finali con cinque pezzi sulla scacchiera. Ciò consente di migliorare la funzione di valutazione e di conoscere i possibili esiti quando l'effetto orizzonte si avvicina alle mosse finali di gioco ( 5 pezzi sulla scacchiera ). I database dei finali sono precalcolati, memorizzati in un database e richiamati dall'algoritmo di ricerca all'occorrenza. Richiedono pertanto una grande quantità di spazio a disposizione per essere memorizzati e archiviati sul computer.
Estensione singola. L'estensione singola è la migliore mossa in assoluto a partire da una determinata situazione di gioco. Quando questa mossa viene individuata nel corso della ricerca, viene memorizzata per essere approfondita in un secondo momento. Al raggiungimento del limite di profondità della ricerca, l'algoritmo prosegue a scandagliare in profondità soltanto i casi delle estensioni singole per verificare le mosse successive oltre l'effetto orizzonte.
