Induzione a ritroso

L'induzione a ritroso è un metodo di risoluzione dei problemi ( problem solving ) in un gioco sequenziale con informazione completa e razionalità perfetta dei giocatori. Il metodo consiste nel mettersi dei panni dell'ultimo giocatore a muovere, analizzare la sua mossa razionale e da quest'ultima risalire progressivamente "a ritroso" alle scelte precedenti dell'altro giocatore, fino a ricostruire l'iterazione strategica più razionale del gioco. Il processo di induzione a ritroso si conclude quando l'induzione giunge alla mossa del giocatore che muove per primo. Nel seguente grafo è ricostruita una situazione di gioco sequenziale a due turni tra due giocatori ( G₁ e G₂ ). Il giocatore G₁ è indicato con i cerchi blu, il giocatore G₂ con i quadrati rossi. Nelle ultime scelte, sulla destra, è indicato il pay-off che ottengono i giocatori alla fine del gioco.

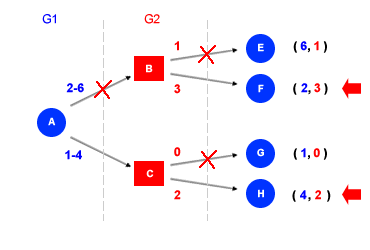
Le ultime scelte migliori del giocatore G₂ ( rosso ) sono le scelte F ed H dove ottiene rispettivamente un pay-off pari a +3 ( F ) e +2 ( H ). Risalendo a ritroso analizziamo le precedenti scelte più razionali del giocatore G₁ ( blu ). Il giocatore G₁ può scegliere tra B e C. Nel primo caso ( B ) può ambire a un pay-off da 2 a 6, mentre nel secondo caso ( C ) a un pay-off da 1 a 4. Il giocatore G₁ sa bene che se scegliesse B ( pay-off più alto ) non potrebbe mai ottenere +6 ( E ) ma soltanto +2 ( F ) poiché nella mossa successiva il giocatore G₂ sceglierebbe l'opzione F in quanto, dal suo punto di vista, offre un pay-off superiore (3 ) rispetto all'opzione E ( 1 ). Scegliendo l'opzione C, invece, il giocatore G₁ è sicuro di poter raggiungere un pay off superiore pari a +4 ( H ). In conclusione, malgrado la scelta B sia apparentemente quella migliore ( strategia dominante ), al giocatore G₁ conviene razionalmente scegliere l'opzione C ( strategia dominata ) per ottenere un vantaggio superiore alla fine del gioco. Il metodo dell'induzione a ritroso è utilizzato nella teoria dei giochi per spiegare la formazione delle strategie decisionali in economia politica e nei sistemi di intelligenza artificiale.

Strategie dominate. Il metodo dell'induzione a ritroso consente di evitare gli errori più comuni delle strategie dominanti. La selezione delle strategie dominanti, o l'eliminazione delle strategie dominate, non assicura il raggiungimento di un equilibrio o di un risultato ottimale. Ad esempio, se le scelte iniziali fossero basate soltanto sulla selezione della strategia dominante, nell'esempio precedente il giocatore G₁ avrebbe scelto l'opzione B e ottenuto un pay-off di +2 ( F ).

Razionalità perfetta. L'induzione a ritroso implica la razionalità perfetta degli agenti decisionali. Ogni agente deve scegliere l'opzione che massimizza il suo risultato finale ( utilità ). La razionalità perfetta non è una caratteristica degli esseri umani ed è, pertanto, poco realistica. Non consente di interpretare la realtà dei fenomeni economici e sociali.

Informazione completa. L'induzione a ritroso implica l'informazione completa di entrambi i giocatori. Per poter scegliere la strategia migliore il giocatore G₁ deve necessariamente conoscere i pay-off finali del gioco. In caso contrario non potrebbe in alcun modo prevedere le scelte successive del giocatore G₂ e, quindi, nemmeno il risultato finale del gioco. Nella realtà, quasi tutti i problemi della vita quotidiana sono caratterizzati da informazione imperfetta e incompleta.

Complessità e completezza. Il metodo dell'induzione a ritroso implica l'analisi completa dell'albero di gioco. Per poter conoscere le ultime scelte di gioco è necessario esplodere tutte le possibili combinazioni del gioco. Ciò diventa particolarmente complesso, sia dal punto di vista spaziale che temporale, quando le opzioni di scelta sono molte e il processo decisionale è molto lungo. Anche utilizzando un computer l'enumerazione di tutte le combinazioni di un problema complesso potrebbe richiedere enormi risorse sia in termini di spazio di memoria che di tempo di elaborazione.