Teorema di Chebyshev
Secondo il matematico russo Chebyshev, data una distribuzione X di valori con un valore medio μ e una costante λ maggiore di zero (λ>0 ), la percentuale di elementi compresa nell'intervallo μ-λσ, μ+λσ è almeno 1-1/λ2.
La formula di Chebyshev
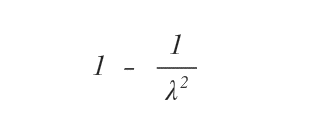
Nota. Il simbolo sigma (σ) è la deviazione standard della distribuzione X ossia lo scarto quadratico medio della variabile casuale.
La probabilità che si estragga dalla variabile casuale X un valore compreso tra μ-λσ, μ+λσ è superiore a 1-1/λ2
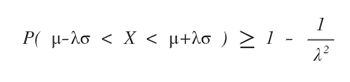
Indipendentemente da come sono distribuiti i valori nella distribuzione X, dalla disuguaglianza di Chebyshev si deduce che
- almeno il 75% dei valori sono compresi tra μ − 2 σ e μ + 2 σ
- almeno l'89% dei valori sono compresi tra μ − 3 σ e μ + 3 σ
- almeno l'94% dei valori sono compresi tra μ − 4 σ e μ + 4 σ
- almeno l'96% dei valori sono compresi tra μ − 5 σ e μ + 5 σ
Il teorema di Chebyshev è anche detto diseguaglianza di Bienaymé-Chebyshev.
Un esempio pratico
Data una popolazione X qualsiasi e una costante λ=3, secondo il teorema di Chebyshev si può stimare che almeno l'89% degli elementi della distribuzione siano compresi nell'intervallo μ-λσ, μ+λσ.
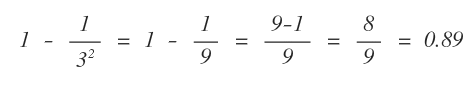
Pertanto, l'89% degli elementi della distribuzione è compresa tra μ-3σ, μ+3σ.
Il restante 12% si trova al di fuori di questo intervallo, a destra e a sinistra.
Il caso della distribuzione normale
In una distribuzione normale o poco asimmetrica si può affermare che:
- il 68% degli elementi della distribuzione è osservato entro l'intervallo μ-σ, μ+σ
- il 95% degli elementi della distribuzione è osservabile entro l'intervallo μ-2σ, μ+2σ ( doppia devianza standard )
- il 99% degli elementi della distribuzione è osservabile entro l'intervallo μ-3σ, μ+3σ ( tripla devianza standard )
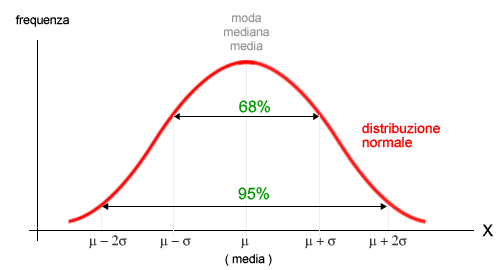
Nota. Una distribuzione normale è perfettamente simmetrica a destra e a sinistra del valore medio.
