Teorema di Bayes
Il teorema di Bayes in statistica consente di calcolare la probabilità condizionata di una causa di un evento A noto B, a partire dalla conoscenza delle probabilità a priori degli eventi A e B della probabilità condizionata di B noto A. Il teorema di Bayes viene sviluppato da Thomas Bayes ed è conosciuto anche come teorema della probabilità delle cause. La formula del teorema di Bayes ( regola di Bayes ) può essere scritta nel seguente modo:
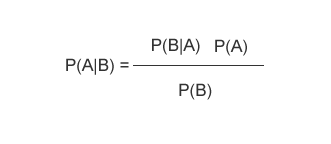
Il teorema di Bayes è utilizzato in molti campi. Ad esempio, nella diagnosi medica il teorema di Bayes consente di calcolare la probabilità di una malattia in una persona che presenta determinati sintomi, a partire dalla frequenza della malattia e dal grado di efficacia del test diagnostico.
Dimostrazione del teorema di Bayes
Il teorema di Bayes può essere dimostrato a partire dal teorema della probabilità assoluta e dal teorema della probabilità composta.
Il teorema di Bayes può essere dimostrato anche a partire dalle probabilità condizionate di due eventi A e B nel seguente modo:
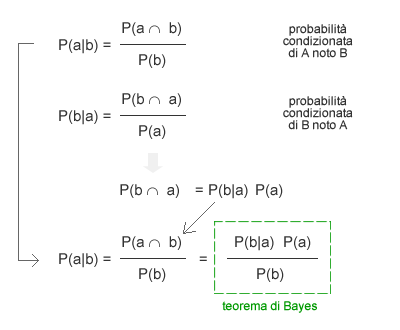
La formula generale di Bayes normalizzata
La formula generale di Bayes normalizzata è la seguente:
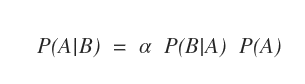
Dove α è la costante di normalizzazione che permette di ottenere una somma degli elementi P(A|B)=1.
Esempio di normalizzazione
Nel seguente esempio si applica un fattore moltiplicativo α=2 per trasformare i valori delle probabilità <0.4 , 0.1> in modo tale da avere una somma uguale a 1 mantenendo le stesse proporzioni <0.8, 0.2>.
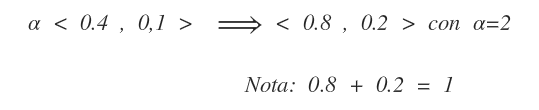
In questo modo si può affermare che l'evento ha l'80% di probabilità di verificarsi e il 20% di non verificarsi.
Applicazioni del teorema di Bayes. In campo diagnostico sono note le frequenze degli eventi e le probabilità condizionate delle relazioni causali. Questi dati sono utilizzati per calcolare la probabilità di un evento su un singolo soggetto.
- Esempio di applicazione del teorema di Bayes. Ad esempio, la malattia M colpisce una persona su 1000 con una probabilità assoluta P(M). Un particolare sintomo S si presenta in una persona su 10 con una probabilità assoluta P(S). Nelle persone affette dalla malattia M il sintomo S si presenta nel 50% dei casi con una probabilità condizionata P(S|M). Per calcolare la probabilità che la presenza del sintomo S in un soggetto ( paziente ) indichi anche la presenza della malattia M, si ricorre alla formula di Bayes. In base al teorema di Bayes la probabilità condizionata P(M|S) è pari al 1% ( p=0,01 ).
