Probabilità
La probabilità è un numero reale P compreso tra 0 e 1 inclusi che esprime il grado di possibilità di un evento casuale ( evento aleatorio ) di verificarsi. Essendo sempre compresa tra zero e uno, la probabilità può essere rappresentata anche in forma percentuale.
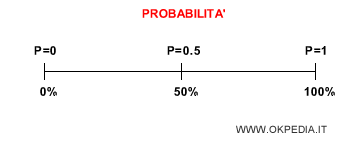
Gli estremi della probabilità sono l'evento impossibile e l'evento certo.
- Evento impossibile. Il valore minimo zero ( p=0 ) indica l'impossibilità che l'evento si verifichi.
- Evento certo. Il valore massimo della probabilità è uno ( p=1 ) e indica la certezza che l'evento si verifichi ( evento certo ).
La teoria delle probabilità ( o calcolo delle probabilità ) è la disciplina matematica che studia la probabilità dei fenomeni statistici prevedibili.
Quando un fenomeno è prevedibile? Un fenomeno statistico è prevedibile con buona approssimazione quando si ripete nel tempo con discreta regolarità ( es. margine di errore di una macchina, gioco di carte, ecc. ). Pertanto, la probabilità può essere calcolata soltanto per un sottoinsieme di fenomeni statistici caratterizzati da ripetibilità e regolarità.
Un esempio pratico di calcolo della probabilità
Ad esempio, un dado ha sei facce. Dopo aver lanciato il dado, la probabilità che esca una determinata faccia del dado ( es. il numero sei o il numero due, ecc. ) è pari a una su sei, ossia p=1/6 ( p=0,17 ).
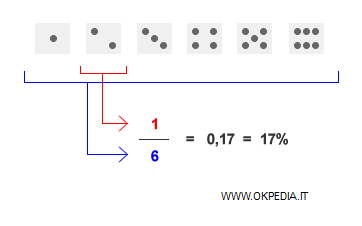
In teoria, nel 17% dei lanci del dado si presenterà la faccia del dado auspicata dal lanciatore.
La differenza tra probabilità empirica e formale
Esistono due definizioni di probabilità basate su due metodi di calcolo diversi.
- Probabilità formale. La probabilità formale di un evento E è il rapporto tra il numero casi possibili favorevoli ( r ) e il numero complessivo dei casi possibili ( k ).
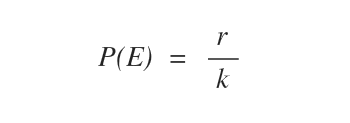
Esempio. Il dado ha 6 facce ( 6 casi possibili ). La probabilità formale che esca il numero due ( 1 caso favorevole ) è pari a 1/6 ossia il 17% ( p=0.17 ).
- Probabilità empirica. La probabilità empirica di un evento E è la frequenza relativa con cui si verifica un caso durante le N prove di un esperimento. È determinata dal rapporto tra il numero dei successi ( S ) e il numero complessivo delle prove ( N ).
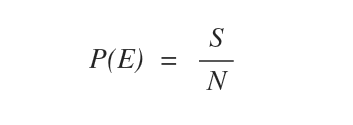
Esempio. Un giocatore lancia 100 volte il dado e 22 volte esce la faccia con il numero due. In questo esperimento la probabilità empirica del numero due è pari a 22/100 ossia il 22% ( p=0.22 ).
La probabilità empirica e la probabilità formale si basano su due distinti metodi di calcolo. Pertanto, forniscono due probabilità diverse per lo stesso evento.
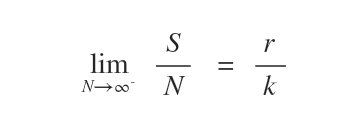
Tuttavia, al crescere delle N prove empiriche la probabilità empirica tende ad avvicinarsi alla probabilità formale.
Esempio. Lanciando il dado 1000 volte, la probabilità empirica che esca il numero due tende a eguagliare la probabilità formale ossia 1/6. Lo stesso vale per qualsiasi altra faccia del dado.
Probabilità di successo e insuccesso
La probabilità di successo di un evento è il rapporto tra il numero dei casi favorevoli e il numero dei casi possibili o totali. È indicata con la lettera p.
$$ p = \frac{s}{n} $$
La probabilità di insuccesso di un evento è la differenza tra 1 e la probabilità di successo p. È indicata con la lettera q.
$$ q = 1 - n $$
Nota. La somma della probabilità di successo (p) e di insuccesso (q) è uguale a uno. Per fare una dimostrazione basta svolgere i passaggi algebrici dell'espressione q+p ossia (1-p)+p che, una volta semplificata, diventa pari a 1
Il pronostico
Il pronostico è la proporzione tra la probabilità di successo (p) e la probabilità di insuccesso (q).
$$ p : q $$
Esempio. Se la probabilità di successo è del 60% e la probabilità di insuccesso è del 40%, il pronostico dell'evento è 6:4 ossia 3:2. Si legge "tre a due".
Il pronostico contro è, invece, la proporzione tra la probabilità di insuccesso (q) a la probabilità di successo (p) ossia q : p.
Le scuole del calcolo delle probabilità
Ci sono diversi approcci allo studio del calcolo probabilistico. I principali approcci sono i seguenti:
- Scuola frequentista. Secondo la scuola frequentista la probabilità deriva dalle prove sperimentali. Dato un campione di oggetti è possibile calcolare la frazione di questi che rispondono a una determinata caratteristica e, quindi, stimare la probabilità sull'intera popolazione.
Esempio. Osservando un campione di gatti randagi in un quartiere, è possibile stimare che il 10% dei gatti della città è di colore nero.
- Scuola oggettivista. Secondo la scuola oggettivista le probabilità sono parte della natura stessa degli oggetti e della natura. In un ambiente macroscopico l'incertezza deriva dalla mancanza di informazioni sui fenomeni da parte dell'osservatore.
Esempio. Lanciando una moneta si ha il 50% di ottenere testa e il 50% croce. Tuttavia, avendo tutte le informazioni a disposizione sulla forza del lancio, la gravità, il vento, la superficie, ecc. sarebbe possibile sapere con certezza quale faccia si presenterà dopo il lancio.
Viceversa, in un ambiente microscopico ( es. quantistico ) tutti i fenomeni hanno una natura probabilistica e l'incertezza non deriva dall'assenza di informazioni ma è essa stessa una parte integrante della realtà.Esempio. Non si può conoscere con precisione l'orbita di un elettrone di un atomo perché può percorrerne molteplici allo stesso modo. In questo caso l'incertezza è insita nel fenomeno fisico. Non dipende dalla scarsa conoscenza del fenomeno.
- Scuola soggettivista. Secondo la scuola soggettivista la probabilità deriva dalla credenza di un individuo ( soggetto ) su un particolare fenomeno. In condizioni di incertezza una persona ha un margine di dubbio sulle proprie affermazioni e le accompagna con una valutazione probabilistica ( es. "secondo me il fenomeno al 90% dipende da questa cause" ).
Esempio. Se l'automobile non parte, l'automobilista può pensare che potrebbe trattarsi della batteria scarica al 40% dei casi o un guasto elettrico al 20%, ecc. Sulla base dei sintomi di un paziente, un medico può ipotizzare che si tratti di una particolare malattia nel 10% dei casi. In questo caso non si tratta di percentuali frequentiste, basate sull'osservazione generale di un campione e riconosciute da tutti, bensì di percentuali determinate dall'esperienza soggettiva e dalla credenza della persona su un determinato fenomeno.
- Secondo Pierre Laplace ( 1819 ) la teoria della probabilità è il buon senso trasformato in un metodo di calcolo.
- Secondo James Maxwell ( 1850 ) la vera logica su cui si basa il mondo è il calcolo delle probabilità.
- La probabilità formale ed emprica sono la stessa cosa?
No, la probabilità formale ed empirica sono una diversa metodologia di calcolo della probabilità statistica.
