Distribuzione binomiale
La distribuzione binomiale è uno strumento del calcolo combinatorio che permette di calcolare la probabilità di successo P(x) in N prove ripetute di un esperimento, quando sono soddisfatte le seguenti condizioni:
- ogni prova ha soltanto due esiti possibili
- le prove sono indipendenti tra loro
- la probabilità p di ogni prova è costante
La formula della distribuzione binomiale
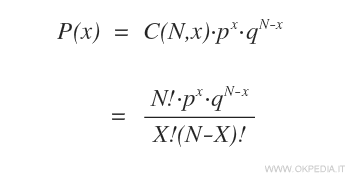
Dove p è la probabilità di successo della singola prova, x è il numero della prova ( da 1 a N ), q è la probabilità di insuccesso (1-p), C(N,x) sono le combinazioni possibili.
Nota. La distribuzione binomiale è ideata dal matematico Jean Bernoulli nel XVII secolo. Per questa ragione è conosciuta anche come distribuzione di Bernoulli.
Un esempio pratico
In un'urna sono presenti 10 palline, 7 di colore rosso e 3 di colore blu.
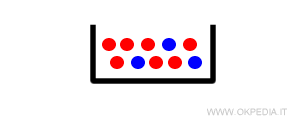
Un esaminatore compie tre estrazioni ( prove ) a campione.
In ogni prova, l'esaminatore estrae una pallina e poi la rimette nell'urna.
Qual è la probabilità di estrarre soltanto una pallina rossa (X=1) in tre estrazioni (N=3) consecutive?
Il calcolo della distribuzione binomiale è il seguente:
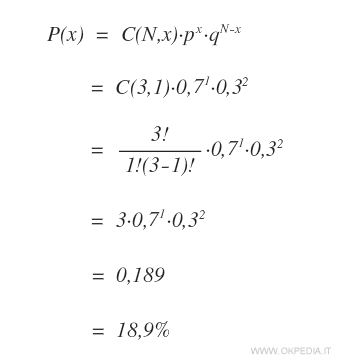
La probabilità di estrarre soltanto una pallina rossa in tre prove è 0,189 ossia il 18,9%.
Qual è la probabilità di estrarre due palline rosse (X=2) in tre estrazioni (N=3) consecutive?
Il calcolo della probabilità secondo il metodo di Bernoulli è il seguente:
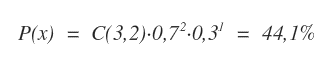
La probabilità di estrarre due palline rosse in tre prove è pari al 44,18%.
Nota. La probabilità di estrarre due palline è maggiore rispetto a una sola, perché nell'urna le palline rosse sono molte di più rispetto a quelle blu. È quindi più probabile estrarne due rosse (44,1%) che due blu e una rossa (18,9%).
Le distribuzioni di Bernoulli
La distribuzione binomiale è una distribuzione discreta della probabilità.
Al variare del numero delle prove positive (x) e della probabilità di successo (p) la distribuzione assume una curva differente.
Caso 1: probabilità 0.5
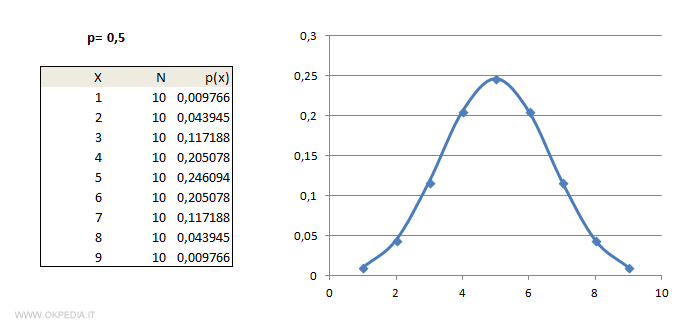
Caso 2: probabilità al 75%
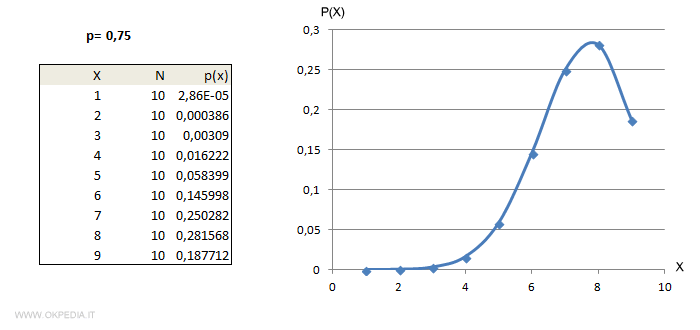
Caso 3: probabilità al 25%
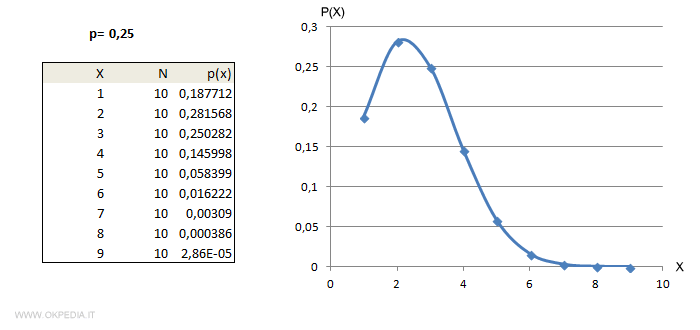
Nota. La distribuzione binomiale non è utilizzabile quando il campione è estratto da una popolazione finita senza reinserimento degli elementi estratti, perché gli eventi non sono indipendenti. In questi casi occorre usare la distribuzione ipergeometrica. Tuttavia, se il campione estratto è molto piccolo rispetto alla popolazione ( meno del 5% ) il margine di errore è limitato ed è preferibile usare la distribuzione binomiale perché più facile da calcolare.
FAQ
- Come calcolare la distribuzione binomiale su Excel?
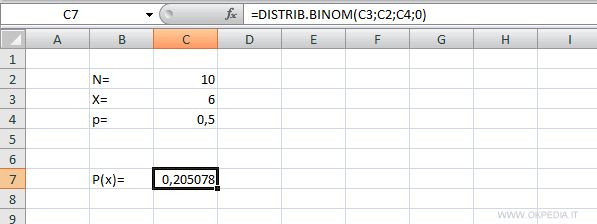
Per calcola la distribuzione di Bernoulli su un foglio elettronico si può costruire una formula usando la funzione delle combinazioni. La formula funziona su Microsoft Excel, Open Office Calc e Google Fogli.
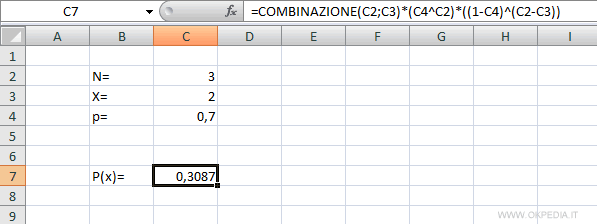
In alternativa si può anche usare la formula DISTRIB.BINOM() nella forma non cumulativa su Excel, la formula BINOMDIST su Google Fogli.