Distribuzione ipergeometrica
La distribuzione ipergeometrica è uno strumento di calcolo combinatorio per calcolare la probabilità di successo P(x) in N prove ripetute durante un esperimento, quando le prove non sono indipendenti.
La formula della distribuzione ipergeometrica
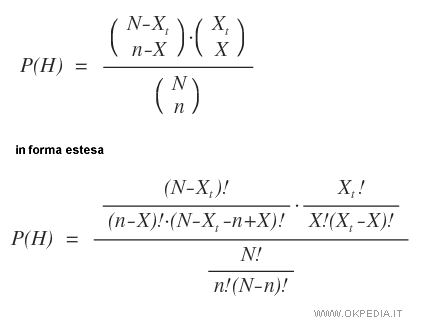
Legenda
N=popolazione
n=campione di n elementi
Xt=successi potenziali nella popolazione N
X=successi potenziali nel campione n
La distribuzione ipergeometrica calcola la probabilità discreta del numero dei successi X in un campione di n elementi selezionati casualmente e senza reinserimento da una popolazione di N elementi.
Esempio di prove non indipendenti. L'estrazione delle palline da un'urna senza reinserimento è un esempio classico di prova non indipendente, perché un'estrazione influenza le probabilità delle estrazioni successive.
Un esempio pratico
In un'urna ci sono 5 palline rosse e 5 palline blu.
Si tratta di una popolazione finita con N=10.
Dall'urna estraiamo 6 palline senza reinserirle nell'urna ( n=6 ).
Qual è la probabilità di estrarre 2 palline rosse?
Il numero dei successi che vogliamo misurare è indicato nella variabile X=2.
Essendoci cinque palline rosse nell'urna, il numero dei potenziali successi è Xt=5.
Calcolando la formula della distribuzione ipergeometrica si ottiene:

La probabilità di estrarre due palline rosse (X=2) in un campione di sei elementi (n=6) è pari al 24%.
La differenza tra distribuzione binomiale e ipergeometrica
La principale differenza tra la distribuzione binomiale e la distribuzione ipergeometrica è la seguente:
- La distribuzione binomiale si utilizza quando le prove sono indipendenti. Ad esempio, è il caso di estrazione di una pallina con reinserimento nell'urna.
- La distribuzione ipergeometrica si utilizza quando le prove non sono indipendenti. Ad esempio, è il caso di estrazione di una pallina senza il reinserimento nell'urna.
Nota. Quando il campione n è molto piccolo rispetto alla popolazione ( inferiore al 5% ) la differenza tra le due distribuzioni è minima. In tali casi è consigliabile utilizzare la distribuzione binomiale anche se le prove non sono indipendenti, perché il calcolo è più semplice.
Quando la distribuzione ipergeometrica coincide con la distribuzione binomiale?
La distribuzione ipergeometrica e binomiale sono uguali quando il campione estratto è composto da un solo elemento (n=1).
