Distribuzione di probabilità
La distribuzione di probabilità è un modello che associa una probabilità a ogni modalità osservabile di una variabile aleatoria ( o variabile casuale ).
Esempio di distribuzione di probabilità. La distribuzione di probabilità dei punteggi ottenibili con il lancio di due dadi è la seguente:
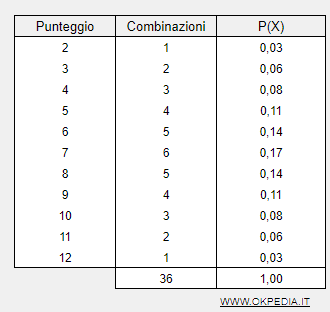
La somma dei valori di una distribuzione di probabilità è sempre uguale a uno.
Tipi di distribuzioni di probabilità
A seconda della natura della variabile casuale, discreta o continua, la distribuzione di probabilità può essere:
- Distribuzione di probabilità discreta
Il fenomeno è osservabile con un numero intero di modalità.Esempio. Il lancio del dado è un fenomeno statistico discreto perché il numero delle modalità osservabili è pari a 6. La variabile aleatoria K può assumere soltanto sei valori { 1, 2, 3, 4, 5, 6 }. Pertanto, la distribuzione di probabilità del fenomeno è discreta.
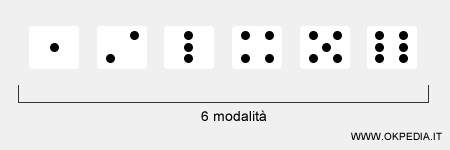
- Distribuzione di probabilità continua
La distribuzione di probabilità è continua quando la variabile casuale assume un insieme continuo di valori. Il fenomeno statistico è osservabile con un numero infinito o troppo elevato di modalità.
Esempio. La distribuzione di probabilità della temperatura corporea è continua perché si tratta di un fenomeno statistico continuo, i valori della variabile aleatoria variano in modo continuo ( es. 36.1°C, 36.2°C, ecc. ).
La funzione di probabilità
La distribuzione di probabilità discreta è espressa tramite una funzione di probabilità p(x) che associa ogni modalità alla relativa probabilità di manifestarsi.
Generalmente consiste in un diagramma a barre oppure a torta.
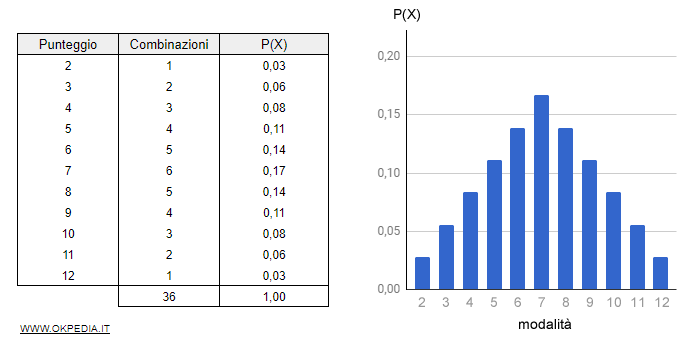
Nota. Il lancio di due dadi è un fenomeno statistico discreto perché le modalità ( punteggio ) sono complessivamente undici. Pertanto, può essere rappresentato con un diagramma a barre con 11 colonne.
La distribuzione di probabilità continua, invece, è espressa tramite una funzione di densità di probabilità f(x).
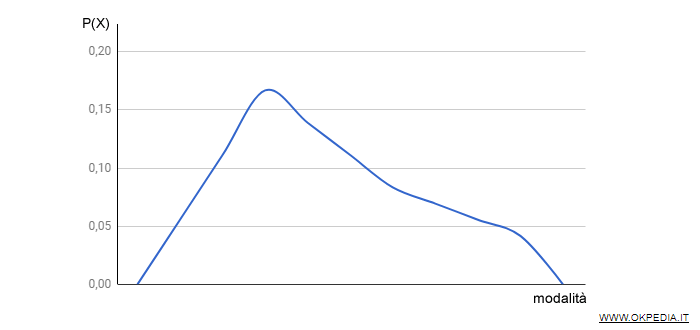
Nota. Trattandosi di un fenomeno statistico continuo, il fenomeno è rappresentabile con una funzione matematica continua.
Un esempio pratico di distribuzione di probabilità
In questo esercizio analizziamo la distribuzione di probabilità nelle famiglie con tre figli.
Con quale probabilità una famiglia ha tre figli maschi o tre figlie femmine? Con quale probabilità ha due figli maschi e una femmina? Con quale probabilità ha due figlie femmine e un maschio?
Partiamo dal presupposto che la probabilità semplice di avere un figlio maschio o femmina è pari 1/2 ossia è il 50% ( P = 0.5 ).
La probabilità composta di una famiglia con tutti figli maschi ( MMM ) è pari a 1/2 X 1/2 x 1/2 ossia P = 0.125 ( 12.5% ).
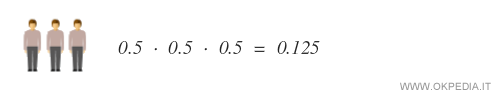
Lo stesso può dirsi per la famiglia con tutte figlie femmine ( FFF ). La probabilità è sempre 0.125 ossia 12.5%.
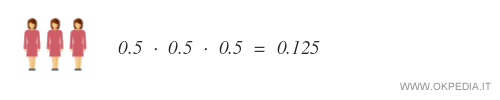
Il calcolo della probabilità di avere due figli maschi ( MM ) e una femmina ( F ) è invece più complesso, perché questa modalità comprende 3 disposizioni semplici ( MMF , MFM , FMM ) in base all'ordine di nascita dei figli.
Esempio. Potrebbero nascere prima due maschi e poi una femmina. In alternativa, potrebbe nascere prima una femmina e poi due maschi. E così via. La combinazione è sempre la stessa ( due maschi e una femmina ) ma le disposizioni sono diverse.
Pertanto, la probabilità di avere due figli maschi e una femmina è pari a 0.375 ossia 37.5%.
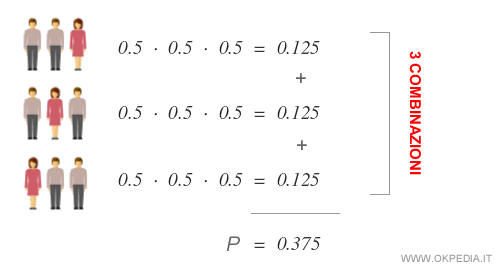
Lo stesso calcolo deve essere effettuato per calcolare la probabilità di avere due figlie femmine ( FF ) e un maschio ( M ). Anche in questo caso ci sono tre combinazioni possibili ( FFM , FMF , MFF ) in base all'ordine di nascita.
Quindi, la probabilità di avere due figlie femmine e un maschio è pari a 0.375 ossia 37.5%.
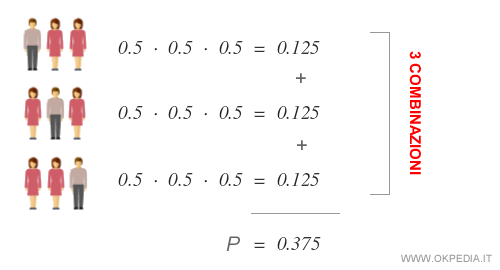
A questo punto abbiamo ottenuto le probabilità P per tutte le quattro modalità M del fenomeno statistico.
Possiamo rappresentare la distribuzione di probabilità sotto forma di tabella.
Nota. La somma delle probabilità P(X) delle modalità è uguale a 1.
La rappresentazione grafica della distribuzione di probabilità
Possiamo rappresentare la distribuzione di probabilità con un diagramma a barre ( o istogramma ) perché si tratta di una distribuzione discreta. È composta soltanto da quattro modalità.
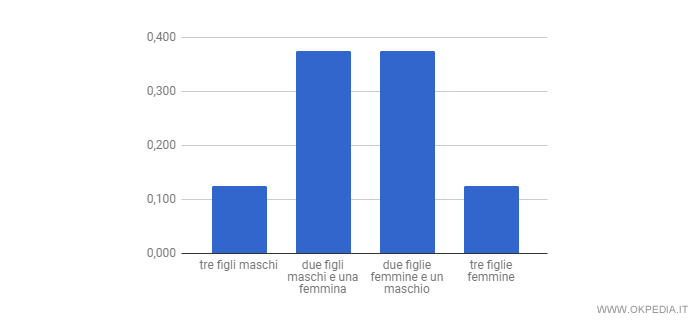
In alternativa, essendo molto poche le modalità statistiche, la distribuzione di probabilità può essere rappresentata graficamente anche con un diagramma a torta.
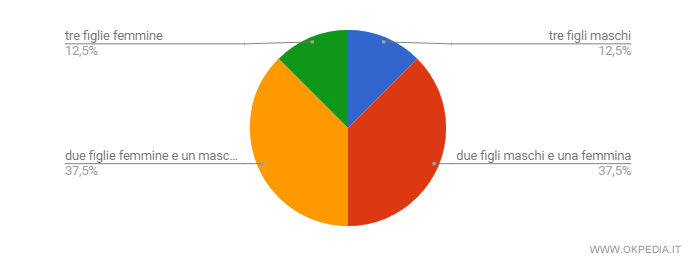
La differenza tra distribuzione di probabilità e di frequenza. La rappresentazione grafica delle distribuzioni è simile ( diagrammi, istogrammi, torte, tabelle, ecc. ) ma la grandezza rilevata è diversa. La distribuzione di probabilità associa ogni modalità X alla relativa probabilità P(x), mentre la distribuzione di frequenza si associa ogni modalità X alla relativa frequenza F(x).
