Variabile aleatoria
Una variabile aleatoria può assumere diverse modalità entro una gamma di valori in funzione di in un particolare fenomeno aleatorio ( casuale ). È anche detta variabile casuale ( v.a. ) o variabile stocastica ( v.s. ).
Esempio. La variabile casuale X contiene le modalità { 1, 2, 3, 4, 5, 6 } ottenibili dal lancio di un dado. Non sappiamo quale faccia del dado uscirà dopo il lancio, ma sappiamo con certezza che sarà una delle sei modalità della variabile casuale X.
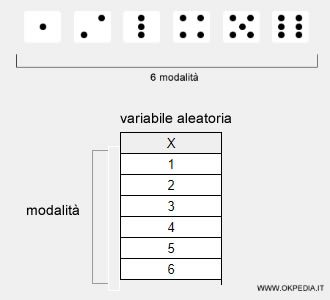
Nella teoria della probabilità la variabile aleatoria è il risultato di un evento non deterministico, ossia incerto e non prevedibile.
La definizione di variabile aleatoria
La definizione formale di variabile casuale ( o aleatoria ) è la seguente:
Dato uno spazio campionario { Ω } composto dalle n-ple combinazioni della variabile statistica K, in cui è definita una misura di probabilità P, la variabile casuale X è una funzione misurabile dallo spazio campionario { Ω } a uno spazio E.
Ad ogni elemento dello spazio campionario { Ω } è associato uno e un solo valore che la variabile casuale X può assumere nello spazio E.
La precedente definizione è una generalizzazione della definizione di Lindgreen.
 Definizione di Lindgreen. Una funzione X definita sullo spazio campionario {Ω} si dice misurabile rispetto al campo di Borel β se e solo se l'evento {ω ∈ Ω : X(ω) ≤ λ } appartiene a β per ogni λ.
Definizione di Lindgreen. Una funzione X definita sullo spazio campionario {Ω} si dice misurabile rispetto al campo di Borel β se e solo se l'evento {ω ∈ Ω : X(ω) ≤ λ } appartiene a β per ogni λ.
Tipi di variabili aleatorie
A seconda della natura del fenomeno che misura, la variabile aleatoria è detta:
- Variabile aleatoria discreta
Quando la variabile aleatoria assume valori in corrispondenza di un insieme finito e misurabile. - Variabile aleatoria continua
Quando la variabile aleatoria assume valori in corrispondenza dell'insieme dei numeri reali R.
La distribuzione di probabilità
La distribuzione di probabilità di una variabile aleatoria X è una funzione che associa a ogni modalità di X la relativa probabilità P(X) di manifestarsi.
Un esempio pratico
La variabile aleatoria X contiene le modalità possibili del lancio di un dado.
Ogni faccia del dado ha una probabilità semplice P(X) di manifestarsi pari a 1/6 ossia circa P(X) = 0.17 ( il 17% ).
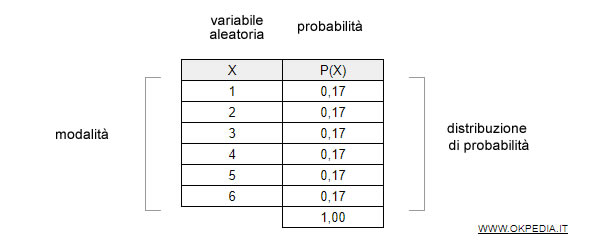
Associando le probabilità a ogni modalità si ottiene la distribuzione di probabilità della variabile aleatoria.
La somma delle probabilità della distribuzione è sempre uguale a 1.
Le variabili aleatorie semplici e multiple
Le variabili casuali sono dette semplici o multiple in relazione alla dimensione:
- Variabili aleatorie semplici ( o univariate ) sono variabili casuali a una dimensione.
- Variabili aleatorie multiple ( o multivariate n-ple ) sono variabili a più dimensioni.
Il processo stocastico
Il processo stocastico è una variabile aleatoria in funzione del tempo ( t ) preso come variabile indipendente.
- Dominio della variabile. Ogni variabile casuale ha un dominio di valori che può assumere. Sulla base del dominio la variabile casuale può essere considerata booleana, discreta o continua.
- Variabile casuale booleana. Una variabile casuale booleana può assumere soltanto due valori: vero o flso. Ad esempio, se una variabile può assumere soltanto i valori vero o falso, il suo dominio è un insieme composto da due elementi { true, false }.
- Variabile casuale discreta. Una variabile casuale discreta può assumere diversi valori. Tutti i valori sono enumerati in modo esaustivo nel dominio della variabile. Ad esempio, la variabile casuale delle condizioni meteorologiche ha un dominio uguale all'insieme { pioggia, sereno, coperto, neve, variabile }.
- Variabile casuale continua. Una variabile casuale continua può assumere un insieme infinito di valori. La distribuzione probabilistica di una variabile casuale continua è infinita e può essere rappresentata soltanto sotto forma di una funzione parametrica ( funzione di densità ) i cui valori sono distribuiti tra il valore minimo e il valore massimo, in modo uniforme o meno. Ad esempio, una variabile casuale continua può avere un dominio uguale a un sottoinsieme di numeri reali. Dati due numeri reali r0 e r1, è sempre presente un numero reale intermedio r2 tale che r0 < r2 < r1.
