Rete bayesiana
La rete bayesiana è una rappresentazione grafica delle relazioni di dipendenza tra le variabili di un sistema. In statistica la rete bayesiana è utilizzata per individuare più agevolmente le relazioni di dipendenza assoluta e di dipendenza condizionale tra le variabili, al fine di ridurre il numero delle combinazioni delle variabili da analizzare.
Ad esempio, la distribuzione congiunta completa delle probabilità di quattro variabili booleane (a, b, c, d) è pari a 24 ossia 16. Se una variabile ( es. d ) è indipendente dalle altre, la distribuzione congiunta delle probabilità può ridursi a 23+2 vale a dire 10.
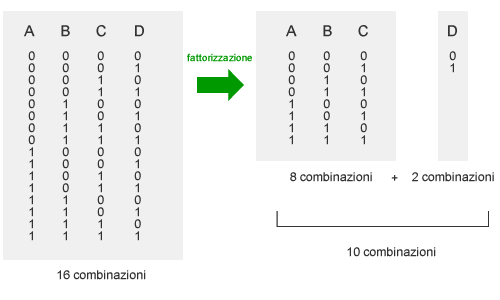
Pur avendo una distribuzione di dimensione inferiore ( 10<16 ), la rete bayesiana offre la medesima completezza di analisi di una distribuzione congiunta completa. La dimensione inferiore della distribuzione probabilistica riduce la complessità, dieci combinazioni anziché sedici, e rende più facile l'analisi del problema.
Il vantaggio di utilizzo delle reti bayesiane cresce con il numero delle variabili. Un problema complesso è caratterizzato da n variabili e analizzare la distribuzione di probabilità congiunta completa è molto difficile quando le variabili del dominio sono molte. Inoltre, spesso non esistono nemmeno dati sufficienti per valutare ogni singola combinazione di eventi ( stati delle variabili ).
La rappresentazione grafica
Dal punto di vista grafico la rete bayesiana è un grafo orientato aciclico ( privo di cicli ) in cui ciascun nodo indica una determinata variabile del sistema mentre gli archi orientati rappresentano le eventuali relazioni di dipendenza ( genitore → figlio ) tra le variabili. L'arco orientato ( freccia ) equivale a dire che il nodo genitore influenza direttamente il nodo figlio ( variabile dipendente ). L'assenza di archi, invece, indica la presenza di una variabile indipendente. Il grafo orientato aciclico è conosciuto anche con l'acronimo DAG ( Direct Acyclic Graph ). L'insieme di archi e nodi è detto topologia della rete. Un esempio di rete bayesiana è il seguente grafo.
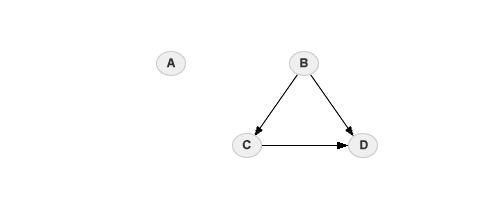
Ad esempio, nel grafo precedente la variabile A è indipendente in quanto il suo nodo è privo di archi ed è isolato dagli altri. La variabile B è, invece, la variabile determinante ( causa ) delle variabili C e D ( variabili dipendenti o effetti ). La relazione di dipendenza di C e D dalla variabile è un tipico caso di dipendenza assoluta ( relazione causale diretta ). È possibile affermare che data la variabile B, la variabile C è indipendente dalla variabile A ( indipendenza condizionale ). Inoltre, è possibile affermare che data B la variabile D è dipendente anche dalla variabile C ( dipendenza condizionale ).
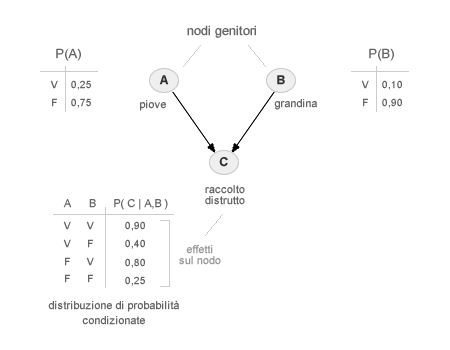
Ogni nodo ha una distribuzione di probabilità condizionate che elenca gli effetti sul nodo in questione, in base ai vari stati che possono assumere i suoi nodi genitori. La tabella della distribuzione delle probabilità condizionate è completa per ciascun nodo.
Tabella delle probabilità condizionate. La tabella delle probabilità condizionate è detta anche CPT. Ogni riga della tabella è uguale uno e, per semplicità espositiva, viene indicato soltanto la probabilità condizionata positiva, quella in cui l'evento si verifica. Se un evento si verifica con probabilità p, questo non si verifica con probabilità (1-p). Quest'ultimo dato si omette nella tabella. Ad esempio, nella rete bayesiana precedente l'evento C si verifica con una probabilità pari a 0,90 quando A e B sono veri. Ne consegue che, nella medesima combinazione di eventi, l'evento C non si verifica nel 10% dei casi ( p=0,10 ).
- Rete causale. La rete bayesiana è anche conosciuta come rete di conoscenza ( o mappa di conoscenza ), rete probabilistica, rete causale. Come reti decisionali le reti bayesiane consentono di studiare le possibili scelte a partire da un determinato evento. Ad esempio, dato un evento causale A ( promozione di Tom ) le probabilità condizionate delle decisioni B ( Tom va in vacanza ) e C ( Tom ottiene un premio ) variano sensibilmente. Se Tom viene promosso nel 90% va in vacanza e nel 10% resta a casa a riposare. Se Tom viene bocciato, al 95% Tom resta a casa a studiare ma nel restante 5% dei casi potrebbe comunque decidere di andare in vacanza. A seconda dell'evento A ( vero o falso ) si presentano due distribuzioni probabilistiche completamente differenti ( scenario 1 e scenario 2 ). La rete decisionale consente di rappresentare graficamente una procedura di inferenza.
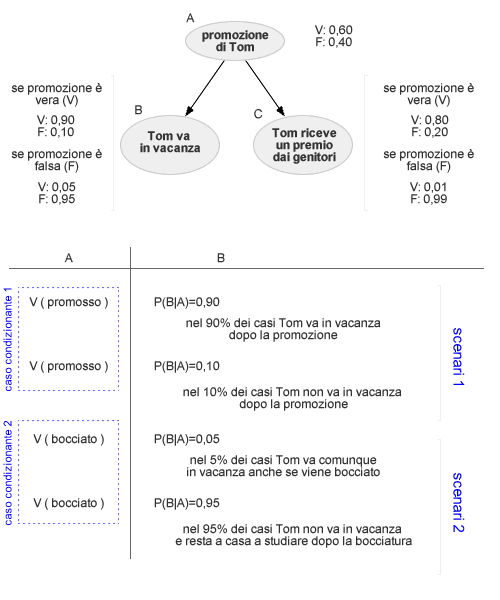
- Rappresentazione della conoscenza in un dominio incerto. Le reti bayesiane sono particolarmente utili nella rappresentazione della conoscenza in situazioni di incertezza. In questo caso i nodi identificano le variabili casuali del problema che, a seconda dei casi, possono assumere valori discreti o continui. Gli archi rappresentano le relazioni causali tra le variabili.
- Altri nomi della rete bayesiana. Una rete bayesiana può essere denominata in vari modi, a seconda del contesto e della materia di studio. Ad esempio, è molto frequente trovare la rete con il nome di mappa della conoscenza, rete causale, rete probabilistica o rete di conoscenza.
- Le reti bayesiane ibride. La rete bayesiana ibrida è una rete composta sia da variabili discrete che da variabili continue. Poiché le variabili continue hanno un dominio di valori infinito, per costruire una rete bayesiana è necessario ridurre il numero dei nodi possibili a un numero accettabile. In tali casi si ricorre a un metodo di discretizzazione.
Le applicazioni delle reti bayesiane
Le reti bayesiane sono utilizzate per la rappresentazione della conoscenza. Possono essere utilizzate per la costruzione di una rete causale o di una procedura di inferenza. In genere, le reti bayesiane sono usate per rappresentare la distribuzione congiunta delle probabilità e per rappresentare le relazioni di interdipendenza condizionale.
- La rappresentazione delle probabilità condizionate ( semantica numerica ). Nell'esempio precedente la probabilità che Tom vada in vacanza si ottiene moltiplicando la probabilità della promozione ( 0,60 ) per la probabilità condizionata che lui decida di andare in vacanza dopo la promozione ( 0,90 ). La partenza di Tom ha una probabilità di verificarsi pari allo 0,54, il dato è ottenuto dal prodotto dei fattori 0,60 · 0,90. Questa applicazione è detta semantica numerica della rete bayesiana.
- La rappresentazione delle relazioni di interdipendenza ( semantica topologica ). Questa applicazione studia le relazioni di indipendenza tra i nodi della rete. Ogni nodo identifica un evento, una particolare situazione o un fatto. Ad esempio, un nodo dipende dai suoi discendenti ma è indipendente da tutti gli altri ( nodi non-discendenti ). Questo consente di realizzare una rappresentazione grafica delle relazioni di indipendenza, detta anche semantica topologica della rete bayesiana.
- Qual è il principale vantaggio dell'uso di una rete bayesiana? La rete bayesiana consente di gestire la rappresentazione di un dominio con molte variabili, in modo più semplice e compatto rispetto alla distribuzione completa delle probabilità. L'organizzazione localmente strutturata dei dati, all'interno delle tabelle CPT, rende inoltre più rapido l'accesso alle informazioni. In termini computazionali la complessità del sistema è inferiore.
- Cos'è l'organizzazione localmente strutturata? I dati del sistema sono assegnati a delle componenti del sistema. Ogni componente è in relazione con pochi altri componenti. Un'eventuale variazione di un dato influisce su un sottoinsieme del sistema e non sull'intero sistema. I sistemi con organizzazione localmente strutturata sono anche detti sistemi sparsi.
- Quando la rete bayesiana coincide con la distribuzione congiunta delle probabilità? Questa situazione si verifica soltanto quando ogni nodo ( variabile ) della rete bayesiana è influenzato da tutti gli altri nodi ( variabili ) della stessa.
- Quando conviene utilizzare la rete bayesiana? Quando ogni variabile del dominio è influenzata da poche altre variabili. A parità di efficacia, quanto più le variabili del problema sono interconnesse tra loro, tanto più si riduce il vantaggio dell'utilizzo della rete bayesiana e aumenta la complessità computazionale.
- Come costruire la rete bayesiana? Per ridurre la quantità delle relazioni tra le variabili, è preferibile iniziare a disegnare la rete a partire dalle cause determinanti ( variabili radice ) e, a partire da queste ultime, sviluppare i nessi verso le variabili infuenzate.
- Cos'è una rete bayesiana ibrida? E' una rete composta sia da nodi-variabili discete e sia da nodi-variabili continue. Una variabile continua può assumere infiniti valori ed è impossibile rappresentare ciascuno di essi sotto forma di nodo. Per la rappresentazione della rete ibrida è necessario ridurre il dominio delle variabili continue, adottando dei metodi di sempliicazione e di discretizzazione.
