La rete bayesiana ibrida
Una rete bayesiana ibrida è composta sia da variabili discrete ( digitali ) che da variabili continue ( analogiche ). Le variabili continue sono molto frequenti nella rappresentazione degli ambienti reali, ad esempio il grado della temperatura.
Per elaborare le variabili continue in una rete bayesiana è necessario trasformarle in variabili discrete, applicando uno dei metodi della discretizzazione. Si può ricorrere a una distribuzione in classi di valori ( es. scaglioni di imposta ) oppure utilizzare una formula matematica basata sulla distribuzione dei valori intorno a un valore medio.
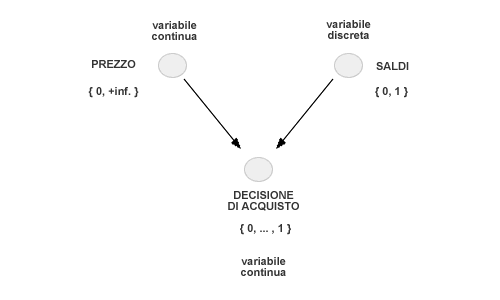
Ad esempio, la decisione di acquisto di un bene da parte di un consumatore è determinata dal prezzo e dalla presenza o meno dei saldi. La decisione di acquisto è una variabile continua, poiché matura gradualmente e il consumatore ci pensa su ed elabora la decisione prima di prenderla, ed è espressa come probabilità condizionata.
P( Acquisto | prezzo, saldi)
Anche il prezzo è una variabile continua, poiché può assumere diversi valori a seconda della concorrenza di mercato. I saldi, invece, sono una variabile discreta poiché sono consentiti per legge soltanto in un particolare periodo dell'anno.
Esistono, quindi, due distinte distribuzioni probabilistiche: una con i saldi e l'altra senza i saldi. La prima è un distribuzione gaussiana ( verde ) condizionata alla presenza dei saldi. La seconda distribuzione ( grigia ) è condizionata all'assenza dei saldi. Come si può notare, in quest'ultimo caso si ipotizza una varianza più ampia.
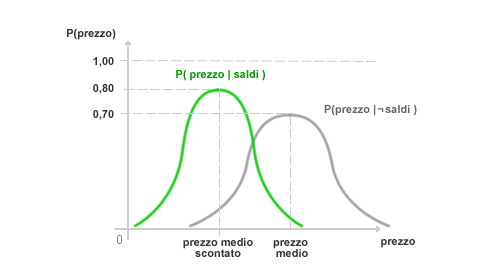
A questo punto occorre costruire una distribuzione probabilistica in relazione alla probabilità di acquisto, a seconda del livello del prezzo e della presenza dei saldi ( effetto psicologico ). Essendoci tre variabili, dovremmo utilizzare una rappresentazione multidimensionale, in questo caso a tre dimensione.
Per semplificare saltiamo questo passaggio e arriviamo direttamente alla relazione diretta tra decisione di acquisto e prezzo, utilizzando due distinte curve di rappresentazione associate alla presenza o meno degli sconti.
La distribuzione gaussiana condizionata delle probabilità di acquisto assume una forma particolare, detta distribuzione probit, in base alla quale la probabilità di acquisto decresce man mano che il prezzo aumenta, in modo brusco.
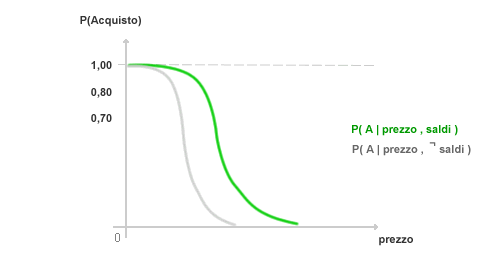
Quando il prezzo si trova nella fascia più ripida, il processo di acquisto è fortemente incerto e le previsioni devono lavorare su una maggiore quantità di ipotesi. Viceversa, agli estremi della curva di distribuzione gli eventi sono caratterizzati da quasi certezza.
Nel grafico le due curve di distribuzione probit sono differenti. In presenza dei saldi ( curva verde ) si aggiunge un effetto psicologico che modifica la propensione di acquisto del consumatore, in quanto è maggiormente spinto ad acquistare qualcosa, pensano di fare un affare.
A differenza della discretizzazione per classi, la distribuzione probit riduce il dominio della variabile continua senza eccessivi tagli o semplificazioni, in modo graduale e morbido. Il metodo si presta ad essere utilizzato nelle rete bayesiane per elaborare le variabili continue. Inoltre, la distribuzione probit semplifica la combinazione lineare dei nodi genitori continui verso un nodo figlio.
La differenza tra distribuzione probit e distribuzione logit
Le due distribuzioni hanno una forma apparentemente simile. La differenza è nel tratto iniziale e/o finale. La distribuzione probit ha una coda più corta che si annulla rapidamente. La curva logit, invece, ha una curva finale molto più lunga.
