Inferenza in una rete bayesiana
Le reti bayesiane possono essere utilizzate per rappresentare i nessi di causalità tra gli eventi e del loro peso probabilistico, all'interno di una base di conoscenza. Sono inoltre uno strumento di inferenza.
A partire da
Un esempio pratico di inferenza
La seguente rete rappresenta i nessi causali tra alcuni eventi. Il sistema è composto da sei variabili booleane ( O, T, B, U, G, I ). Ad esempio, la variabile O è uguale a uno ( 1 ) quando si verifica la crescita del prezzo del petrolio, in caso contrario è zero ( 0 ).
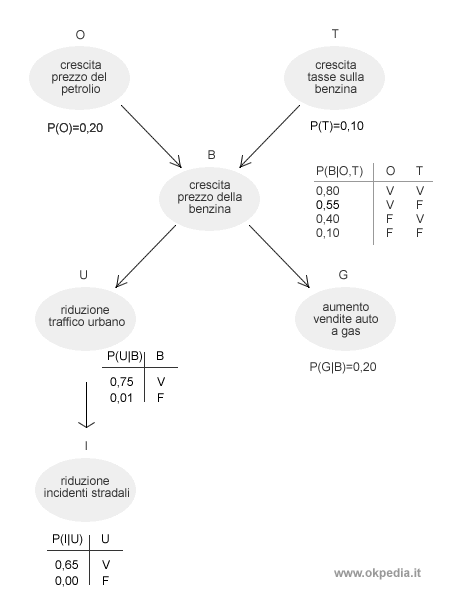
Ogni evento è associato a una probabilità semplice o condizionata. Ad esempio, la crescita del prezzo del petrolio (O) si verifica con una probabilità semplice P(O) pari al 20%. Viceversa, la crescita del prezzo della benzina (B) si verifica con una probabilità condizionata P(O, T) poiché dipende dallo status di altre variabili ( O , T ).
Quanto influisce la crescita delle tasse sulla riduzione degli incidenti stradali?
L'agente razionale si pone questa domanda ( o query ). Per trovare la risposta l'agente può seguire diversi processi. Uno dei più semplici è il processo di inferenza per enumerazione dei fattori rilevanti del problema.
Quali sono le variabili del problema?
Le variabili del problema sono la crescita delle tasse (T) e la riduzione degli incidenti stradali (I). Per variabili di query si intende una variabile a cui è associato un valore di partenza a seconda dell'evento. In questo caso, sia le variabili T e I sono considerate vere.
T=Vero ; I=Vero ;
L'obiettivo del ragionamento è trovare una risposta a variabile di query P(I|T) ossia la probabilità condizionata della riduzione degli incidenti stradali (I) a seguito di un incremento delle accise sulla benzina (T).
P ( I | T )
Quali sono le variabili nascoste?
Come si può notare, le due variabili del problema non sono direttamente collegate tra loro. Esistono pertanto delle variabili nascoste del problema che occorre considerare.
Per trovare le variabili nascoste è possibile risalire le relazioni causali dal nodo figlio ( I ) ai nodi genitori, dal basso verso l'alto, fino a raggiungere la variabile causale ( T ).
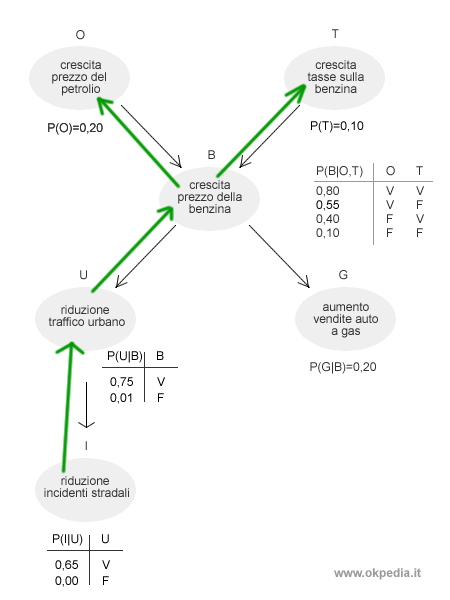
Le variabili nascoste del problema sono l'incremento del traffico urbano (U), l'aumento del prezzo della benzina (B) e del petrolio (O).
Questo metodo inferenziale di enumerazione esatta permette l'esclusione delle variabili irrilevanti come la variabile G ( aumento delle auto a gas ). Sono eliminate automaticamente perché non influiscono sul risultato.
L'enumerazione esatta delle probabilità condizionate
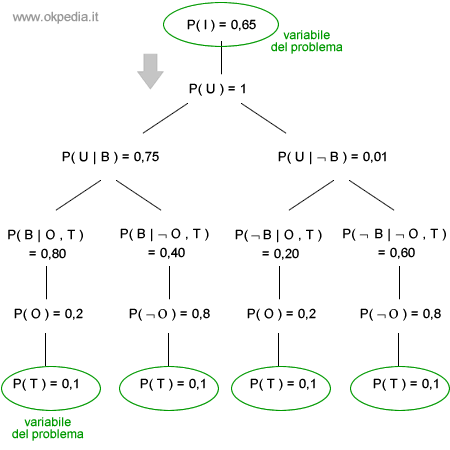
Una volta trovate le variabili del problema ( I, T ) e le variabili nascoste ( O, B, U ) è possibile calcolare la probabilità condizionata dell'evento P ( I | T ). La formula completa della probabilità condizionata dell'evento P ( I | T ) è la seguente:
P ( I | T ) = P ( U | B ) · P ( B | O, T ) · P ( O ) · P ( T )
La figura seguente mostra il cammino necessario per unire le variabili I e T, prendendo come ipotesi il fatto che entrambe siano vere.
Sommando tutte le probabilità condizionate dell'ipotesi P(T)=vero si ottiene un risultato parziale ( subtotale ) pari a 0,02373800 sulla prima tabella.
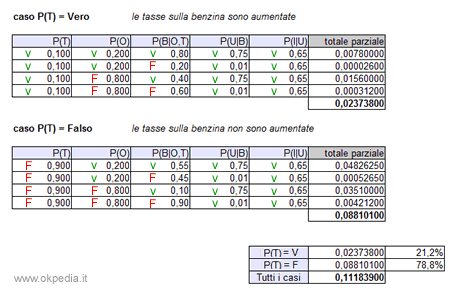
Per calcolare la probabilità condizionata P(I|T) è necessario calcolare anche tutti gli altri casi in cui si verifica una diminuzione degli incidenti ( I=vero ) senza un aumento delle tasse ( T=falso ). Questa seconda ipotesi viene calcolata nella seconda tabella che ha un risultato parziale pari a 0,088101.
Sommando i due risultati parziali ( 0,023738 + 0,088101 ) si ottiene il totale dei casi pari a 0,111839.
A questo punto per ottenere la probabilità condizionata P(I|T) è sufficiente calcolare il rapporto tra il primo subtotale in cui P(T) è vero ( 0,023738 ) e il totale dei casi ( 0,111839 ).
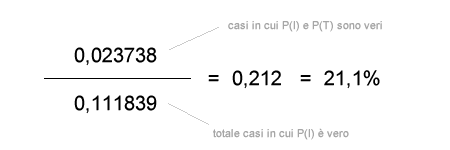
La probabilità condizionata P(I|T) è pari al 21,2%. L'agente può rispondere alla domanda iniziale. Nel 21,2% dei casi in cui si verifica un incremento delle tasse, il numero degli incidenti diminuisce.
I limiti dell'enumerazione completa
Le principali criticità dell'algoritmo di enumerazione sono le seguenti:
- Inefficienza computazionale. L'algoritmo potrebbe richiedere milioni di iterazioni per risolvere un problema più complesso. La complessità spaziale e temporale cresce in modo esponenziale rispetto al numero delle variabili.
- Inefficacia. Se il tempo di elaborazione diventa eccessivo, l'algoritmo potrebbe diventare inefficace. In molti problemi è necessario decidere rapidamente ( es. guida automatica di un veicolo ) e ottenere la soluzione troppo tardi potrebbe essere del tutto inutile.
