Coperta di Markov

La coperta di Markov è uno stato di indipendenza locale di una variabile in una rete bayesiana. Secondo Markov, data una rete bayesiana e un nodo X, quest'ultimo è indipendente da tutti gli altri nodi della rete, dati i suoi nodi genitori, i suoi nodi figli e gli altri nodi genitori dei suoi nodi figli.

Ad esempio, nella seguente rete bayesiana il nodo N₃ ha due nodi genitori ( N₀ e N₁) e due nodi figli ( N₅ e N₆ ), i quali hanno altri due nodi genitori ( N₂, N₄ ). L'insieme di questi nodi è detta coperta di Markov del nodo N₃.

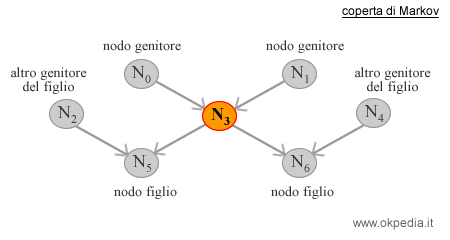
Data la coperta di Markov del nodo N₃, il nodo N₃ è indipendente da tutti gli altri nodi N_x della rete. Qualsiasi modifica alla rete non influisce sul valore del nodo N₃, se la sua coperta di Markov non è intaccata dalla variazione.

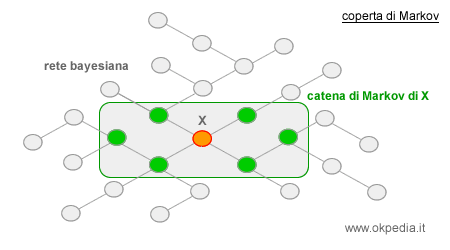
Per questa ragione, si afferma che il nodo X è condizionalmente indipendente da tutti gli altri della rete dentro la sua coperta di Markov. Nella rappresentazione precedente la catena di Markov è identificata dai nodi di colore verde intorno al nodo X.