Catene di Markov
I processi di Markov sono rappresentazioni grafiche dei nessi di causa ed effetto tra le variabili di un sistema. Sono anche noti come catene di Markov. Sono utilizzati per analizzare i problemi, nell'ipotesi che gli stati dell'ambiente operativo siano determinati dagli stati precedenti ( ipotesi di Markov ).
Secondo l'ipotesi di Markov, uno stato corrente è determinanto dagli N stati precedenti. Questa ipotesi semplificatrice consente di analizzare l'evoluzione di un fenomeno, tenendo conto di un insieme finito di variabili e delle regole di funzionamento del sistema.
P(X|Genitori(X))
Se le regole sono chiare e certe, il processo diventa stazionario ed è possibile prevedere ogni stato corrente a partire dagli stati precedenti, secondo un modello di transizione prefissato. La distribuzione della probabilità di un evento nell'istante t è condizionata dagli stati precedenti da 0 a t-1.
P(Xt|X0:t-1)
Questa ipotesi viene proposta per la prima volta dal matematico russo Andrei Markov.
Il grado o ordine dei processi Markov
Nei processi di Markov il grado identifica il numero dei nessi tra uno stato e quelli precedenti.
- Processo di Markov del primo ordine. Nei processi del primo ordine gli stati hanno una relazione di causa ed effetto soltanto con lo stato immediatamente precedente.
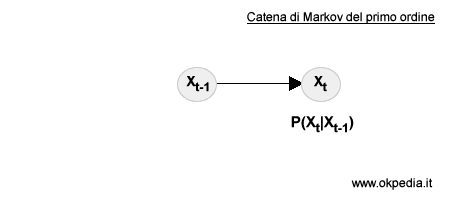
- Processo di Markov del secondo ordine. Nei processi del secondo ordine gli stati hanno una relazione di causa ed effetto con gli ultimi due stati precedenti.
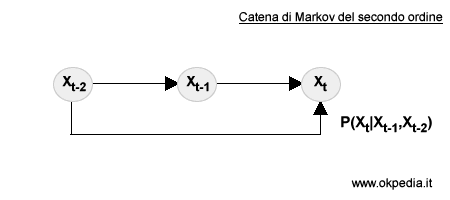
Le catene di Markov del primo e del secondo ordine appartengono ai modelli di transizione, i quali si basano esclusivamente sulle variabili di stato.
A volte le variabili di stato non sono osservabili. In questi casi l'agente razionale deve formulare una previsione sulla variabile di stato utilizzando delle variabili di prova direttamente osservabili. Questi processi appartengono ai modelli sensoriali.
