Principio di indifferenza ( statistica )
Il principio di indifferenza è la distribuzione uniforme della probabilità a priori delle ipotesi su un determinato fenomeno, quando tutte le ipotesi sono mutamente esclusive ( una esclude l'altra ) e non esistono informazioni sufficienti a far preferire un'ipotesi rispetto a un'altra. Il principio di indifferenza viene definito da James Bernoulli nel XVIII secolo. Il medesimo principio viene studiato anche da Laplace con il nome di principio della ragione non sufficiente. Dato un insieme di conoscenza H, in cui gli elementi ( H1, ... , Hn ) sono ipotesi ( proposizioni logiche ) mutuamente esclusive ed esaustive ( se una è vera le altre sono false ), e un insieme di informazioni I di riferimento sul fenomeno, la probabilità di una proposizione ( ipotesi ) è uguale a quella della proposizione simmetrica se non esistono a priori delle informazioni sufficienti a far pensare che una sia favorita rispetto all'altra. Non ci sono ragioni sufficienti per preferire un'ipotesi rispetto a un'altra. In assenza di informazioni sufficienti, essendo tutte le ipotesi simmetriche, da ciò deriva una distrubuzione uniforme della probabilità a priori.
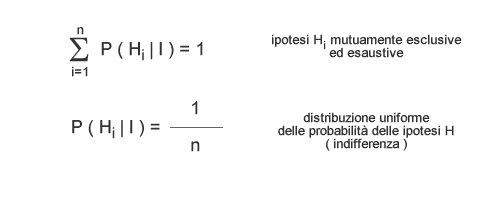
La mancanza di informazioni sufficienti può essere causata dall'ignoranza dell'osservatore sul fenomeno. In tali circostanze l'uomo potrebbe essere costretto a prendere una decisione in tempi rapidi ( es. svoltare a destra o a sinistra ). Non avendo informazioni sufficienti per determinare le probabilità delle ipotesi, considera le probabilità a priori tutte uguali.
