Analisi combinatoria
L'analisi combinatoria è il ramo della matematica che studia il numero dei gruppi costruiti combinando gli elementi di uno o più insiemi di dati secondo regole assegnate.
A cosa serve? Per calcolare la probabilità composta bisogna conoscere tutti gli esiti possibili (k) di un evento. L'analisi combinatoria consente di enumerarli.
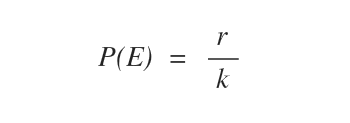
Nei casi più semplici non è difficile conoscere il numero dei casi possibili, mentre nei casi più complessi è necessario calcolarlo con le tecniche dell'analisi combinatoria.
Il principio generale del calcolo combinatorio
Dati due insiemi A e B, se l'insieme A contiene na elementi e l'insieme B ne contiene nb, allora il prodotto cartesiano AxB è composto da tutte le na·nb coppie ordinate (a,b) dove a e b sono gli elementi degli insiemi ( a∈A e b∈B ).
Il principio generale del calcolo combinatorio
Se una prima procedura può essere svolta in n1 modi diversi, una seconda procedura in n2 modi diversi, una terza in n3 modi, ecc. allora il numero totale di modi di realizzazione della procedura è N=n1·n2·n3 ....
Un esempio pratico
Qual è la probabilità di lanciare un dado e una moneta, ottenendo testa e il numero sei?

Per calcolare la probabilità dell'evento p(E) bisogna conoscere il numero dei casi favorevoli r e quello dei casi possibili k.
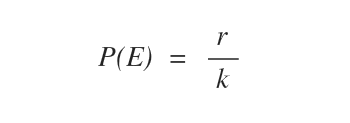
Il numero dei casi favorevoli è uno ( r=1 ).
Si tratta dell'esito sperato in cui la moneta restituisce il lato con la testa e il dado la faccia con il numero sei.
Quanti sono i casi possibili?
Per calcolare il numero dei casi possibili (k) si utilizza l'analisi combinatoria.
Il dado e la moneta sono due eventi distinti.
Il dado è un evento con sei modalità (na=6 ). Ogni faccia del dado è un possibile esito del lancio.
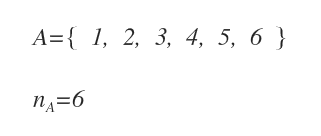
La moneta è invece un evento con due modalità (nb=2 ). Ogni faccia della moneta ( testa o croce ) è un possibile esito del lancio.

Il numero dei casi possibili dei due eventi è na·nb ossia 6x2.
Quindi, il numero dei casi possibili è k=12.
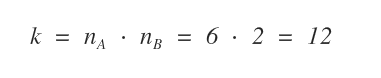
Una volta ottenuto il numero dei casi possibili (k), si può calcolare la probabilità composta dell'evento.
La probabilità composta di ottenere testa e il numero sei è 1/12.
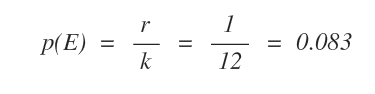
Nota. L'analisi combinatoria ha calcolato il numero dei casi possibili (k) rendendo così possibile il calcolo della probabilità composta dell'evento p(E).
Le combinazioni, disposizioni e permutazioni
Oltre alla probabilità, i principali strumenti dell'analisi combinatoria sono le combinazioni, le disposizioni e le permutazioni.
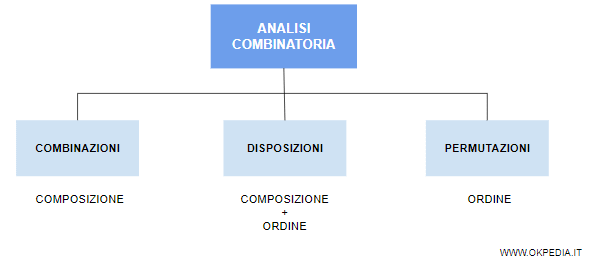
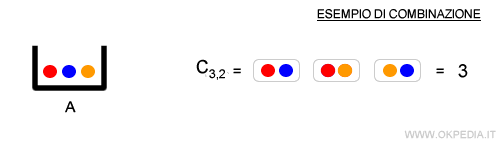
- Le combinazioni. Sono raggruppamenti di k elementi su n che si differenziano per la composizione degli elementi.
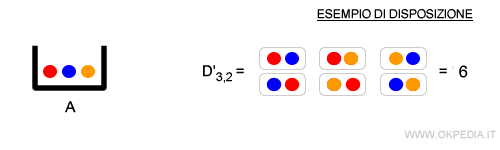
- Le disposizioni. Sono raggruppamenti di k elementi su n che si differenziano tra loro sia per la composizione che per la posizione degli elementi nel gruppo ( o sequenza ).
- Le permutazioni. Sono raggruppamenti di tutti gli n elementi di un insieme che si differenziano tra loro per la posizione degli elementi ossia per l'ordine degli elementi nelle sequenze.
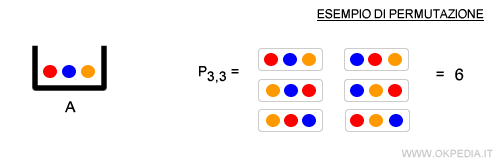
La differenza tra combinazione, disposizione e permutazione. In una combinazione è importante soltanto la composizione del gruppo. In una disposizione conta sia la composizione che l'ordine degli elementi nel gruppo ( o sequenza ). In una permutazione, infine, conta soltanto l'ordine degli elementi nella sequenza.
