Combinazioni
Le combinazioni sono gruppi di k elementi che si possono formare con gli n elementi di un insieme, in modo tale che i raggruppamenti si differenzino tra loro per la composizione senza considerare l'ordine degli elementi.
La formula delle combinazioni senza ripetizione
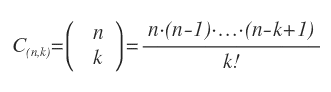
In alternativa la formula può essere rappresentata anche nel seguente modo:
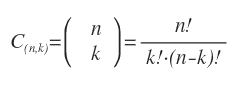
Dove n! è l'n-fattoriale del numero complessivo degli elementi nell'insieme mentre k! è il fattoriale del numero degli elementi nei gruppi.
La formula è detta coefficiente binomiale perché consiste nello sviluppo di una potenza di un binomio.
Un esempio pratico
In un mazzo di carte sono presenti 4 assi.
Quanti sono i tris di assi possibili?
Per rispondere a questa domanda occorre calcolare le combinazioni di k=3 elementi su un insieme di n=4 elementi.
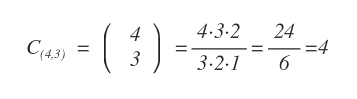
Complessivamente, le possibili combinazioni di tris di assi sono quattro.
Per una rapida verifica.
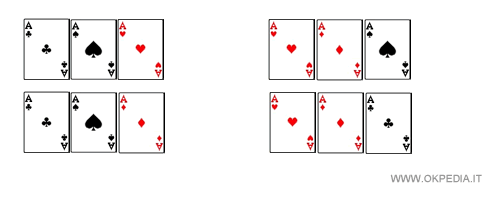
Nota. Nelle combinazioni l'ordine degli elementi non è importante.
Le combinazioni con ripetizione
Quando l'insieme degli elementi è composto da elementi uguali, alcune combinazioni si ripetono.
Per calcolare il numero di combinazioni possibili senza conteggiare le ripetizioni, si utilizza una formula diversa.
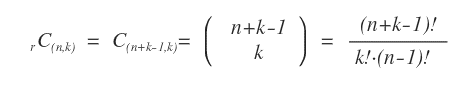
Un esempio pratico
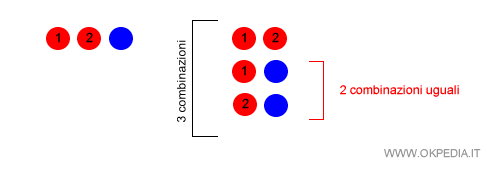
In questo esempio ci sono due palline rosse e una pallina blu.
Le combinazioni senza ripetizione in gruppi di due C(3,2) sono tre.
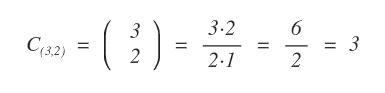
Tuttavia, se osserviamo le combinazioni è evidente la presenza di due combinazioni identiche.

Per calcolare il numero effettivo delle combinazioni si utilizza la formula delle combinazioni con ripetizioni.
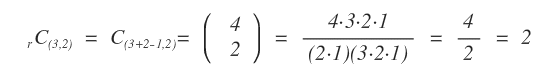
Senza considerare le ripetizioni ci sono soltanto due combinazioni effettive.
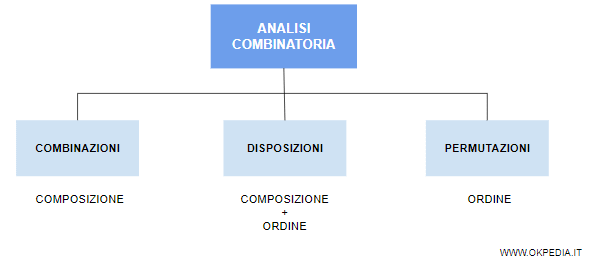
La differenza tra combinazioni, disposizioni e permutazioni
Le combinazioni di k elementi su n (Cn,k) sono uguali al rapporto tra le disposizioni Dn,k senza ripetizione e le permutazioni di k elementi ( k! ).
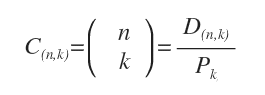
Nota. A differenza delle disposizioni senza ripetizione, le combinazioni non considerano l'ordine degli elementi.
Un esempio pratico
Al cinema sono rimasti 4 posti liberi ma la comitiva di amici è composta da 6 persone. Due persone dovranno rinunciare.
Quante sono le combinazioni?
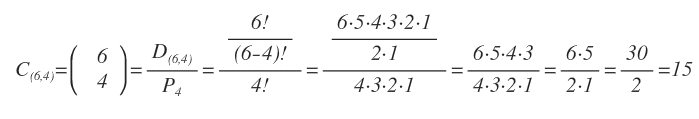
In tutto ci sono 15 combinazioni.
FAQ
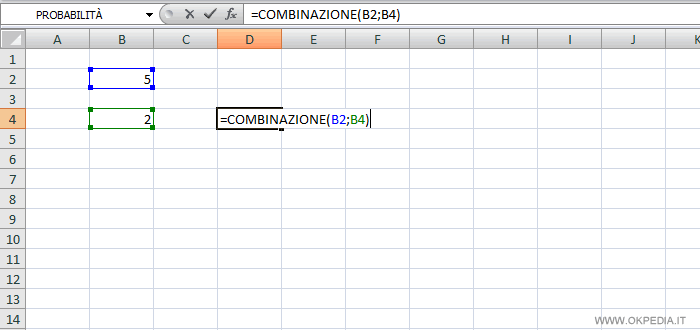
- Come calcolare le combinazioni su Excel?
Nel foglio di calcolo Excel si può calcolare il numero delle combinazioni C(n,k) tramite la formula statistica COMBINAZIONE(n;k). La stessa formula si può usare sul foglio di calcolo Calc di Open Office.
- Qual è la differenza tra combinazioni e permutazioni?
Nelle permutazioni P(n,n) l'ordine degli elementi è un fattore distintivo dei gruppi, mentre nelle combinazioni C(n,k) l'ordine interno degli elementi non è importante. Ad esempio, la differenza tra C(3,3) e P(3,3).
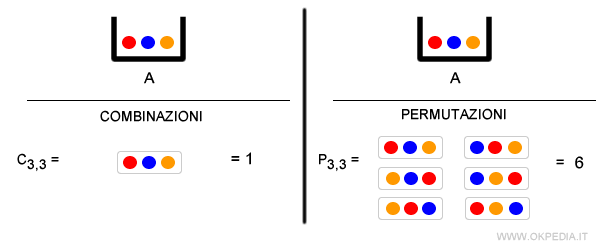
Inoltre, le permutazioni P(n,n) si calcolano su tutti gli n elementi dell'insieme mentre le combinazioni C(n,k) anche su un sottoinsieme k di elementi dove k≤n. -
Quali sono le differenze tra combinazione, disposizione e permutazione?
In una combinazione è importante soltanto la composizione dei raggruppamenti. In una disposizione, invece, conta sia la composizione dei gruppi che la posizione degli elementi all'interno dei gruppi. In una permutazione, infine, conta soltanto la posizione degli elementi ossia l'ordine degli elementi in un gruppo.