Permutazioni
Le permutazioni sono disposizioni senza ripetizione di n elementi in n posizioni, tali che i raggruppamenti differiscano tra loro soltanto per l'ordine degli elementi.

Nota. La permutazione di tutti gli n elementi senza ripetizione è uguale al n-fattoriale ( n! ).
Un esempio pratico
L'insieme A è composto da quattro elementi (n=4).
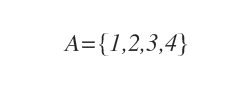
Per conoscere tutte le permutazioni dell'insieme si utilizza la formula seguente:

In questo caso n=4.
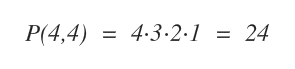
Pertanto, sono possibili ventiquattro permutazioni semplici.

Nota. Le sequenze si distinguono tra loro soltanto per la posizione degli elementi. Inoltre, le sequenze sono composte da tutti gli elementi dell'insieme { 1,2,3,4 }. Ogni elemento compare una sola volta nelle sequenze.
La differenza tra permutazioni e disposizioni
In una permutazione si prendono in considerazioni tutti gli n elementi dell'insieme.
Nella disposizione senza ripetizione, invece, si possono anche raggruppare k su n elementi dell'insieme ( dove k≤n ).
Nota. La permutazione coincide con la disposizione senza ripetizione soltanto in un caso ossia quando k=n.
Infine, in una disposizione con ripetizioni uno stesso elemento può essere ripetuto più volte in diverse posizioni del raggruppamento.
Le permutazioni con ripetizione
Può accadere che un insieme contenga due o più elementi uguali.
In questo caso alcune sequenze delle permutazioni sono uguali.
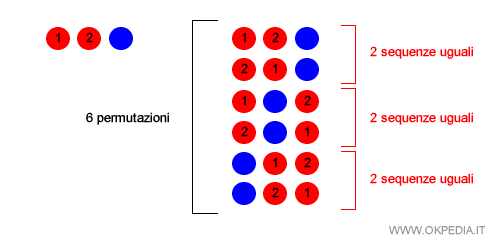
Per calcolare il numero effettivo delle permutazioni, senza le ripetizioni, si ulizza la seguente formula:
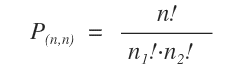
Dove n1! è il fattoriale del numero di elementi di una tipologia ( es. palline rosse ) e n2! è il fattoriale del numero di elementi dell'altro tipo ( es. palline blu ).
Esempio
Nell'esempio precedente ci sono 3 palline, di cui 2 rosse e 1 blu.
Le permutazioni sono sei ma ci sono tre sequenze identiche:

Per calcolare le sequenze effettive si utilizza la formula delle permutazioni con ripetizione.
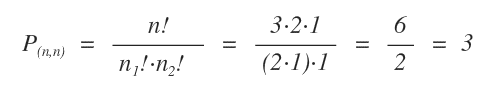
Il calcolo elimina le sequenze uguali.
Effettivamente, ci sono soltanto tre permutazioni diverse tra loro.
