Probabilità composta
La probabilità composta è la probabilità statistica P(A⋂B) che due eventi indipendenti A e B accadano contemporaneamente ( o l'uno dopo l'altro ).
La formula della probabilità composta
La probabilità composta è pari al prodotto delle probabilità dei singoli eventi P(A)·P(B).
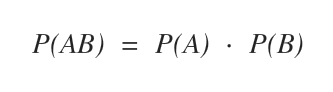
Questa formula della probabilità composta è applicabile soltanto se gli eventi sono indipendenti.
Eventi indipendenti. Due eventi A e B sono detti "indipendenti" se l'esito dell'esperimento A non dipende dall'esito di B, e viceversa. Ad esempio, il lancio di due monete è composto da due eventi indipendenti, perché l'esito della prima moneta ( testa o croce ) non influisce sull'esito della seconda moneta.
Esempio di probabilità composta di eventi indipendenti
Quando si lancia una moneta si ha la probabilità al 50% di fare testa o croce.
Pertanto, quando si lancia la moneta la probabilità di avere testa è p=1/2 ossia p=0.5.
Supponiamo ora di voler calcolare la probabilità di ottenere testa in due lanci consecutivi.
In questo caso abbiamo due eventi consecutivi da considerare ( A e B ).
- La probabilità di avere testa nel primo lancio è P(A)=0.5.
- La probabilità di avere testa nel secondo lancio è P(B)=0.5.
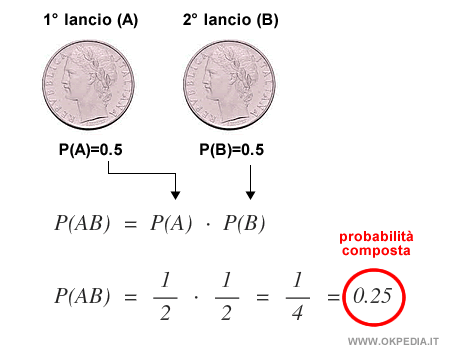
Quindi, la probabilità composta dei due eventi AB è pari a 1/2 x 1/2 = 1/4 ossia P(A⋂B)=0.25.
Nel 25% dei casi lanciando due volte la moneta si ottiene entrambe le volte testa.
Un altro esempio di probabilità composta
Proviamo a calcolare la probabilità di lanciare due dadi e ottenere un punteggio pari a dodici.
Per ottenere dodici con due dadi è necessario che esca il numero 6 su entrambi i dadi.
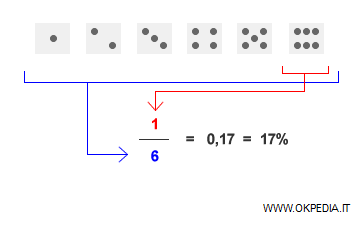
La probabilità semplice di fare 6 con un dado è 1/6 ossia P=0.17.
Anche in questo caso occorre considerare due eventi indipendenti ( A e B )
- La probabilità che esca 6 sul primo dado è P(A)=1/6
- La probabilità che esca 6 sul secondo dado è P(B)=1/6
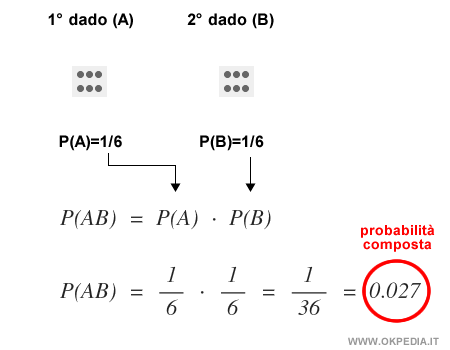
Pertanto, la probabilità composta degli eventi P(A⋂B) è pari a 1/6 x 1/6 = 1/36 ossia P(AB)=0.027.
Nel 2.7% dei casi lanciando due dadi si ottiene il numero dodici.
La probabilità composta degli eventi dipendenti
Quando due eventi A e B sono dipendenti, per calcolare la probabilità composta P(A⋂B) occorre moltiplicare la probabilità del primo evento P(A) con la probabilità condizionata del secondo evento P(B|A) , posto che il primo evento si sia verificato.
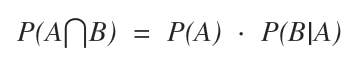
In questo caso la probabilità del secondo evento P(B|A) è influenzata dal primo evento già realizzato (A). La probabilità del primo evento è, invece, semplice e indipendente perché si verifica prima.
Un esempio pratico
Proviamo a calcolare la probabilità di fare ambo a tombola con i primi due numeri estratti.
La probabilità semplice del primo numero estratto è P(A) = 1/90 perché nell'urna ci sono novanta numeri.
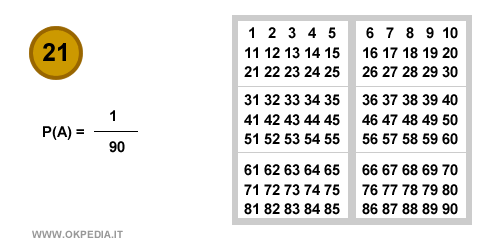
L'estrazione del secondo numero, invece, non ha una probabilità di verificarsi pari a 1/90 perché un numero è già stato estratto dalla urna. Ora nell'urna ci sono 89 numeri ( 90 - 1 ).
Inoltre, ci sono 4 numeri sulla riga con cui poter fare ambo ( 22, 23, 24 e 25 ). Non solo uno.
Pertanto, la probabilità di estrazione del secondo numero P(B|A) è pari a 4/89.
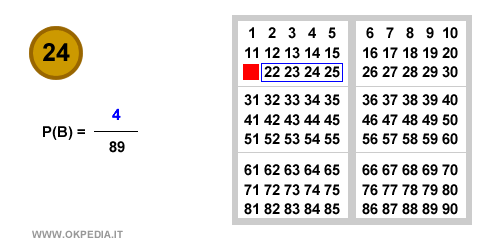
Pertanto la probabilità composta di fare ambo sul cartellone con i primi due numeri estratti è 1/90 x 4/89 ossia P(AB)=0.000499
Questo evento si verifica nello 0.0499% dei casi.
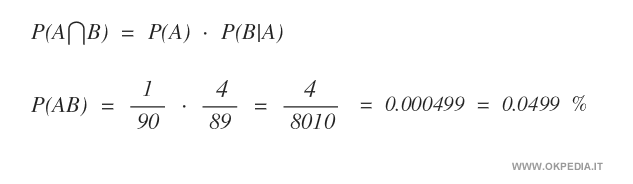
In questo caso la probabilità composta degli eventi non è 1/90 x 4/90 bensì 1/90 x 4/89 perché i due eventi statistici sono dipendenti. Il primo evento P(A) condiziona la probabilità del secondo evento P(B|A). Per questa ragione quest'ultima P(B|A) è detta probabilità condizionata o probabilità a posteriori.
- Probabilità congiunta. La probabilità composta è anche detta probabilità congiunta di due eventi. Ad esempio, dato un problema con due proposizioni x e y. La proposizione x è una variabile casuale discreta delle condizioni meteorologiche { sereno, nuvoloso, pioggia, neve } con una distribuzione probabilistica pari a { 0,40, 0,30, 0,25, 0,05 }. La proposizione y è, invece, una variabile casuale booleana del ritardo del bus { si, no } con una distribuzione probabilistica pari a { 0,20, 080 }. La probabilità congiunta che inizi a piovere quando il bus è in ritardo è pari a 0,25·0,20.
P ( pioggia, ritardo ) = 0,25 · 0,20 = 0,05 = 5%
- Probabilità congiunta completa. La probabilità congiunta completa è la distribuzione delle probabilità congiunte dell'intero insieme di combinazione degli eventi. Nel caso delle variabili casuali discrete è possibile rappresentare l probabilità congiunta mediante una tabella a matrice, come la seguente:
