Distribuzione log-normale
La distribuzione log-normale è una distribuzione statistica non gaussiana di valori con proprietà simili alla distribuzione normale gaussiana.
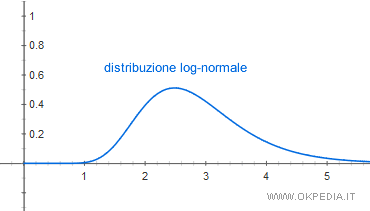
A cosa serve? Una distribuzione log-normale può essere trasformata in una distribuzione normale gaussiana. È così possibile calcolare la probabilità cumulata dei fenomeni.
Le caratteristiche della distribuzione log-normale
Una distribuzione f(x) non è distribuita normalmente.
Se la variabile indipendente x è il logaritmo naturale di y, allora la sua rappresentazione logaritmica f(y)=ln(y) è distribuita in modo log-normale.
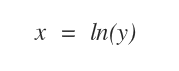
E' quindi possibile usare la sua rappresentazione log-normale per sfruttare le proprietà della distribuzione normale.
La formula della distribuzione log-normale
Nella distribuzione f(x) la variabile casuale è la x.
Se la distribuzione logaritmica y=ln(x) ha una distribuzione normale, la funzione f(y) appartiene alla classe delle distribuzioni log-normali.
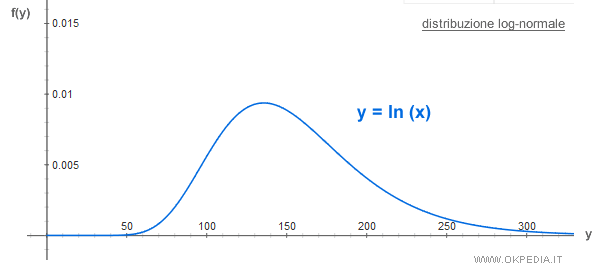
Sostituendo la variabile casuale ln(y) al posto della x nella distribuzione normale si ottiene la formula della distribuzione log-normale:
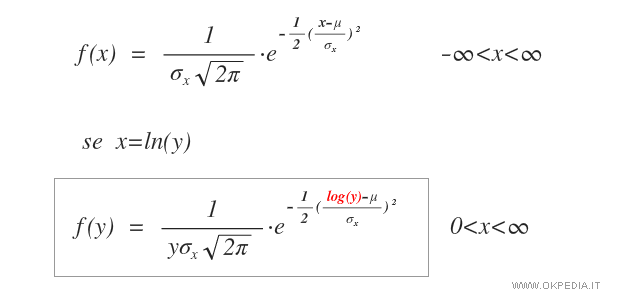
Dove x è la variabile casuale positiva compresa nel range di valori 0<x<∞.
Il simbolo μ è la media e il simbolo σ è la deviazione standard.
Nota. Le distribuzioni log-normali sono molto frequenti nei fenomeni sociali ed economici. La log-normalità è diffusa anche in fisica e in meccanica.
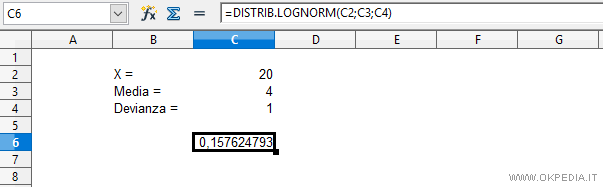
Come calcolare la distribuzione lognormale su Excel
Per calcolare la distribuzione lognormale su un foglio elettronico (Excel, Calc o Google Fogli) si utilizza la funzione DISTRIB.LOGNORM
DISTRIB.LOGNORM(x; media; dev_standard; cumulativo)
I parametri della funzione sono i seguenti:
- X. È il valore della variabile casuale.
- Media. È la media della distribuzione ln(x).
- Dev_standard. È la deviazione standard di ln(x).
- Cumulativo. Se è uguale a 1 restituisce il valore cumulativo della distribuzione, se è uguale a 0 restituisce la funzione di densità della probabilità.
Un esempio pratico