Distribuzione normale
La distribuzione normale è una distribuzione della probabilità continua di un fenomeno statistico intorno alla media. È anche conosciuta come distribuzione gaussiana dal nome del suo autore, il matematico tedesco Gauss, che la formula per la prima volta all'inizio del XIX secolo.
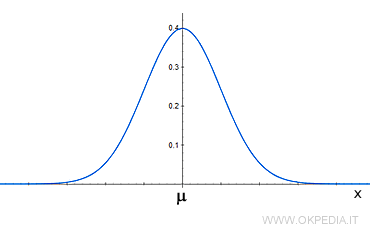
A cosa serve? È la curva della probabilità più usata nell'analisi statistica, perché descrive con discreta efficacia gran parte dei fenomeni naturali. Le probabilità più elevate di un fenomeno si concentrano intorno alla media. Le probabilità si riducono man mano che ci si allontana dal valore medio a destra o a sinistra.
La distribuzione normale delle probabilità rappresentata sul piano cartesiano da una curva a campana, continua e mesocurtica, detta curva gaussiana o curva normale.
Le caratteristiche della curva gaussiana
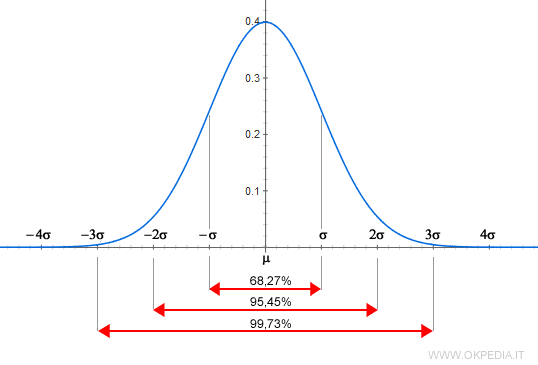
Le principali caratteristiche della curva della distribuzione normale sono le seguenti:
- La frequenza/probabilità più elevata coincide con il valore medio centrale e decresce spostandosi a destra o a sinistra.
- Allontanandosi dalla media la curva si avvicina sempre più all'asse orizzontale delle ascisse, senza mai toccarlo.
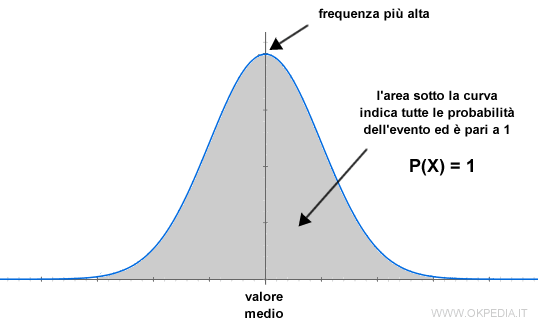
- L'area complessiva sotto la curva normale ( grigia ) è uguale a uno perché comprende tutte le probabilità dell'evento. La superficie sotto la curva si può calcolare con un integrale.
La funzione di densità della probabilità
La probabilità che la variabile X sia compresa in un determinato intervallo ( x1 , x2 ) è uguale alla superficie sottostante la curva di Gauss tra gli estremi ( x1 , x2 ).
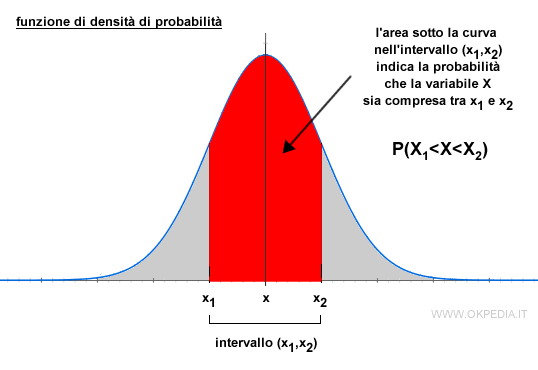
Nel precedente grafico la superficie dell'area rossa è pari alla probabilità P(X1<X<X2).
Per calcolare la superficie si ricorre al calcolo di un integrale definito della funzione f(x).
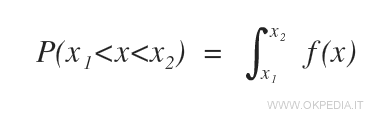
L'area complessiva sotto la curva di Gauss è uguale a 1. Pertanto, qualsiasi superficie delimitata da estremi è compresa tra 0 e 1.
Nota. Se la curva di distribuzione è standardizzata, l'area può essere calcolata più velocemente tramite una tabella di conversione, senza calcolare l'integrale.
La formula della distribuzione normale
Per disegnare il grafico della distribuzione normale si utilizza un'apposita funzione f(x).
La formula della distribuzione normale è la seguente:
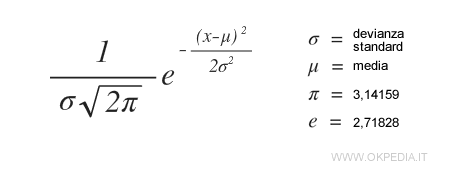
Dove μ è la media della distribuzione e σ è la deviazione standard.
La distribuzione normale standardizzata
La distribuzione normale standardizzata è un caso specifico che si ottiene quando la media è uguale a zero (μ=0) e la deviazione standard è uguale a uno (σ=1).
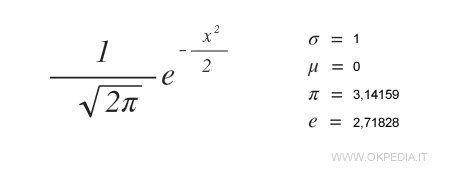
In questo caso la curva della distribuzione è centrata intorno al valore zero (x=0).
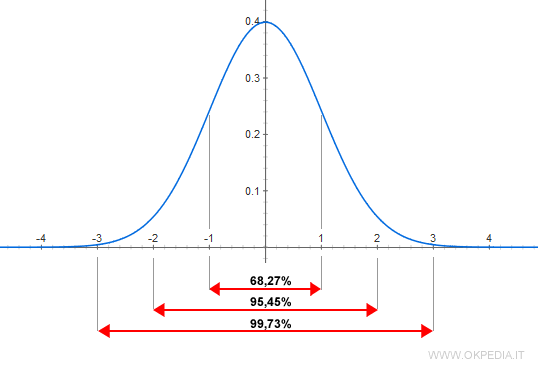
La distribuzione normale standardizzata permette di calcolare l'area sotto la curva gaussiana tra due estremi x1 e x2 tramite una tabella di conversione senza utilizzare il calcolo integrale.
Come funziona la tabella di conversione della distribuzione normale standardizzata
Nella tabella di conversione ogni valore standard dell'unità z è associato a:
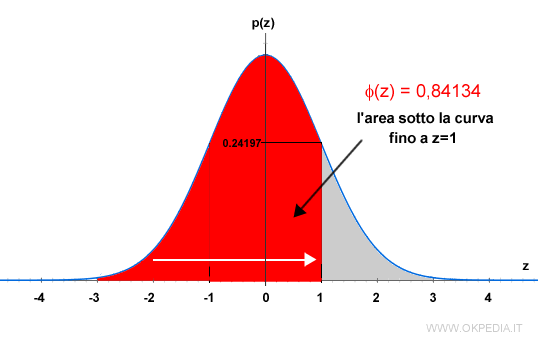
- al valore φ(z) pari all'area compresa tra l'estremo di sinistra della curva di distribuzione e il punto z ( probabilità cumulata )
- al valore p(z) pari all'altezza della curva di distribuzione nel punto z, ossia alla probabilità di p(z).
Ecco un esempio di tabella per i principali valori di z.
| z | φ(z) | p(z) |
|---|---|---|
| -4,00 | 0,00003 | 0,00013 |
| -3,50 | 0,00023 | 0,00087 |
| -3,00 | 0,00135 | 0,00443 |
| -2,50 | 0,00621 | 0,01753 |
| -2,00 | 0,02275 | 0,05399 |
| -1,50 | 0,06681 | 0,12952 |
| -1,00 | 0,15866 | 0,24197 |
| -0,50 | 0,30854 | 0,35207 |
| 0,00 | 0,50000 | 0,39894 |
| 0,50 | 0,69146 | 0,35207 |
| 1,00 | 0,84134 | 0,24197 |
| 1,50 | 0,93319 | 0,12952 |
| 2,00 | 0,97725 | 0,05399 |
| 2,50 | 0,99379 | 0,01753 |
| 3,00 | 0,99865 | 0,00443 |
| 3,50 | 0,99977 | 0,00087 |
| 4,00 | 0,99997 | 0,00013 |
Per vedere la tabella di trascodifica completa clicca qui.
Nota. Per motivi di sintesi alcune tabelle di conversione partono dal valore centrale (0) e mostrano soltanto i valori positivi di z perché i valori negativi sono semplici valori opposti (-z). I valori sono sempre gli stessi. Tuttavia, se si utilizzano queste tabelle bisogna considerare che cambia qualche passaggio aritmetico per calcolare l'area sotto la curva gaussiana.
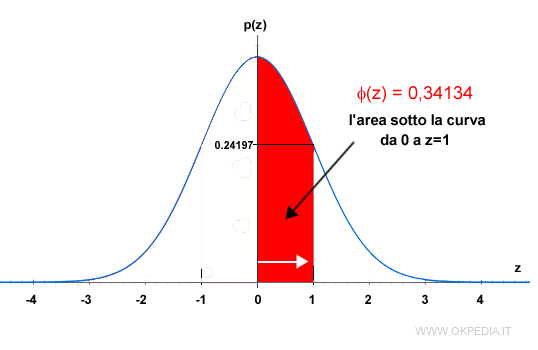
Ad esempio, in questo caso φ(z=1) è uguale a 0.34134 perché parte da zero. Quindi, per calcolare la probabilità cumulata occorre aggiungere anche l'area a sinistra di zero che è pari a 0.5. Quindi, la probabilità cumulata di z=1 è pari a 0.34134+0.5=0.84134. I conti tornano.
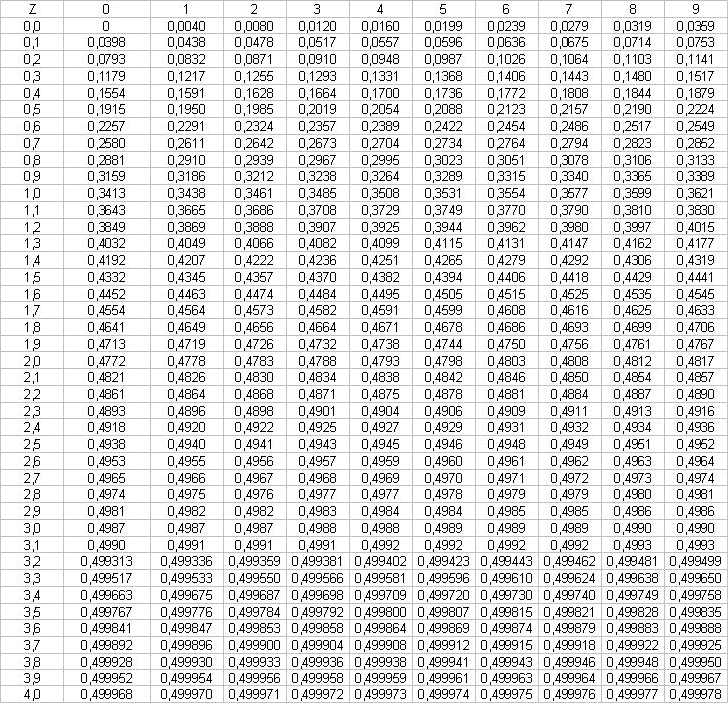
Come si legge la tabella? Ad esempio, per trovare il valore associato a z=1,55. Si cerca la riga z=1,5 poi si scorre a destra fino alla colonna 5 ( ossia +0,05 ). La cella indica il valore associato a z=1,55 che in questo caso è 0,4394. Per trovare il valore negativo si usa lo stesso metodo, aggiungendo il segno meno davanti al valore ossia -0,4394. In entrambi i casi bisogna poi aggiungere +0,5 al valore appena trovato per ottenere la probabilità comulata φ ossia 0,5+0,4394=0,9394 ( per z=1,55) e 0,5-0,4394=0,0606 ( per z=-1,55 ).
Come convertire una distribuzione normale in una distribuzione normale standardizzata
Qualsiasi distribuzione normale può essere convertita in una distribuzione normale standardizzata tramite l'utilizzo di una variabile in unità standard ( z ).
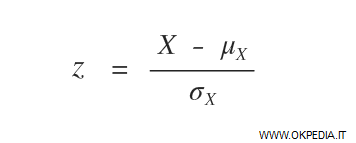
Dove X è il valore della variabile, μ è la media e σ è la deviazione standard.
Un esempio pratico
Nel suo curriculum universitario uno studente ha la media del 25 dei voti e una devianza standard pari a 3.6.
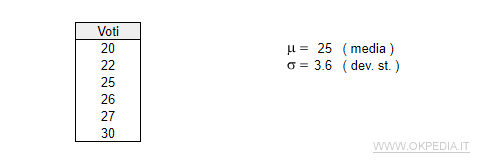
Qual è la probabilità di prendere un voto tra 28 e 30?
Per il calcolo utilizziamo la formula della distribuzione normale standardizzata.
Quindi, calcoliamo l'unità z per gli estremi x1=28 e x2=30.
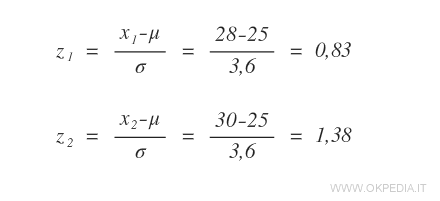
Abbiamo così trovato i valori standardizzati della variabile x misurati con l'unità standard z.
Ora cerchiamo le due grandezze z1 e z2 nella tabella di conversione per individuare le relative probabilità cumulate φ(z) in una distribuzione normale.
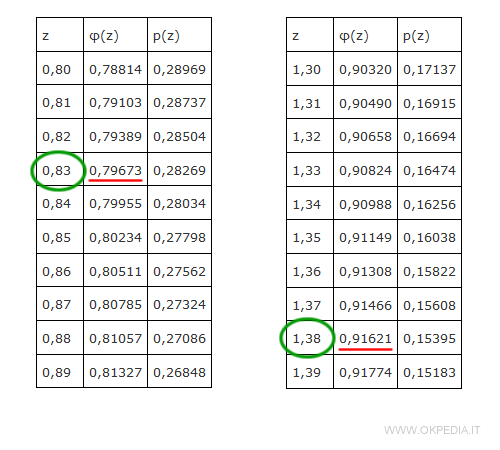
Le probabilità cumulate φ(z1) e φ(z2) misurano rispettivamente l'area sotto la curva di distribuzione fino a z1 e z2 a partire da sinistra.
In questo modo si evita di dover calcolare l'integrale della funzione.
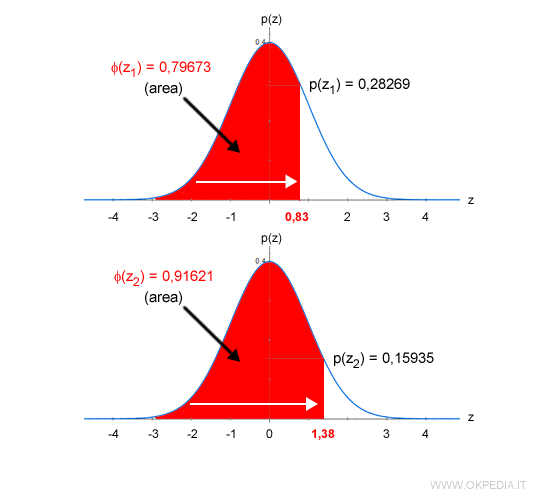
Per ottenere la superficie sotto la curva da z1 e z2 è sufficiente una semplice sottrazione tra le probabilità cumulate φ(z2) - φ(z1).
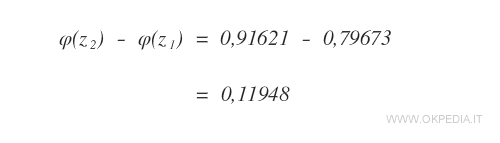
Si ottiene così l'area (rossa) della sezione che ci interessa ossia la probabilità cumulata da z1 e z2.
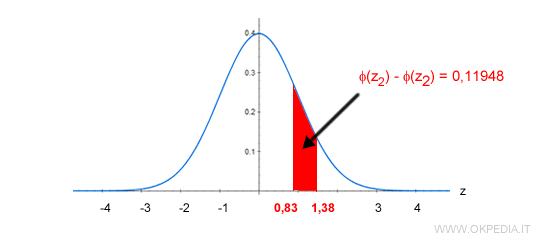
Secondo la distribuzione normale, la probabilità che lo studente prenda un voto tra 28 e 30 è pari al 11,94% ossia p=0,11948.
Nota. La tabella di transcodifica è molto utile perché evita di calcolare l'integrale definito. Tuttavia, la conversione è approssimativa perché considera soltanto le prime 5 posizioni decimali del numero. Per questa ragione, il calcolo della probabilità può differire leggermente.
Faq
Come calcolare la distribuzione normale su Excel
Per calcolare la distribuzione normale su un foglio elettronico ( Excel, Calc o Google Fogli ) si utilizza la funzione DISTRIB.NORM.
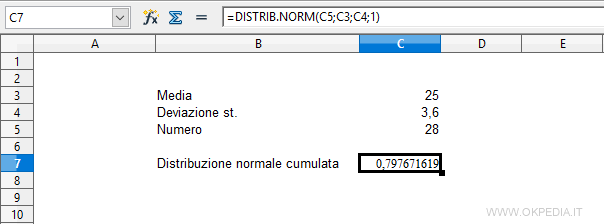
La funzione ha quattro parametri
DISTRIB.NORM(Numero; Media; Deviazione standard; Cumulata)
- Numero. È il numero di cui si vuole calcolare la probabilità.
- Media. È la media della distribuzione.
- Deviazione Standard. È la deviazione standard della distribuzione.
- Cumulata. Va indicato 1 per avere la probabilità cumulata. Se è indicato 0 ( o nulla ) restituisce l'altezza della curva a campana.
Come calcolare la distribuzione normale standardizzata su Excel
Per il calcolo della distribuzione normale standard su un foglio elettronico ( Excel, Calc, Fogli ) si utilizza la funzione DISTRIB.NORM.ST
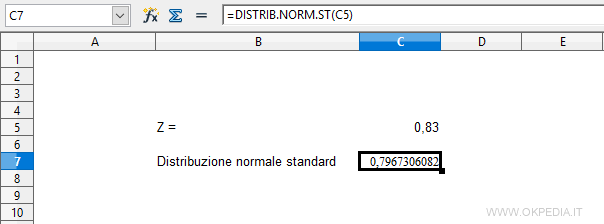
La funzione ha un solo parametro.
DISTRIB.NORM.ST(Numero)
- Numero. È il valore della variabile standardizzata (z). Dove z=0 è il valore centrale della distribuzione.
