Curtosi
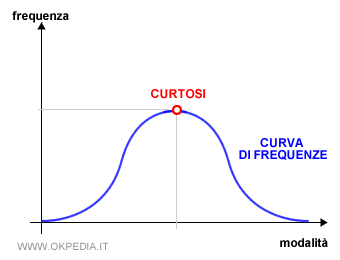
La curtosi è l'altezza massima raggiunta nella curva di frequenze di una distribuzione statistica. La rappresentazione grafica della curtosi consente di comprendere la natura e le caratteristiche dell'intera distribuzione e del fenomeno statistico.
Esempio. La sequente distribuzione raggiunge la curtosi nel punto A.
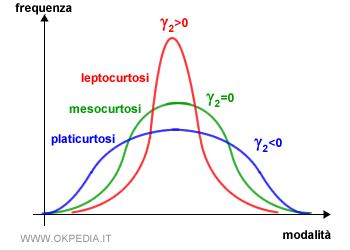
Le principali tipologie di curtosi sono la leptocurtosi, la platicurtosi e la mesocurtosi.
Leptocurtosi
La leptocurtosi è una curva di frequenza con una curtosi molto alta. È detta curva leptocurtica.
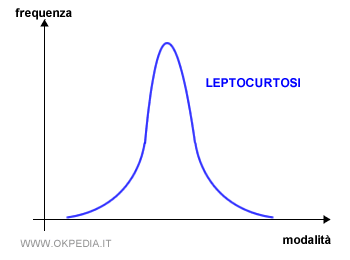
In questo caso, gli elementi della distribuzione sono concentrati nelle immediate vicinanze della media aritmetica. La variabilità è minima.
Esempio. La distribuzione d'età in una classe della prima elementare è leptocurtica perché gran parte degli alunni ha la stessa età.
Mesocurtosi
La mesocurtosi è una curva di frequenza con una distribuzione normale. È detta curva mesocurtica.
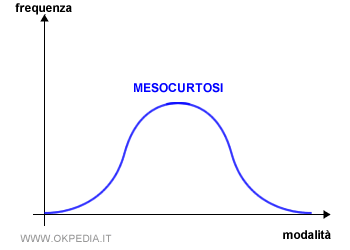
Gli elementi della distribuzione si distribuiscono in modo normale intorno alla media in modo simile, ma non necessariamente uguale, a una curva gaussiana.
Esempio. La distribuzione dell'età dei giocatori di basket professionisti si distribuisce in modo normale intorno alla media aritmetica.
Platicurtosi
La platicurtosi è una curva di frequenza con una distribuzione quasi piatta. La curtosi è molto bassa. È detta curva platicurtica.
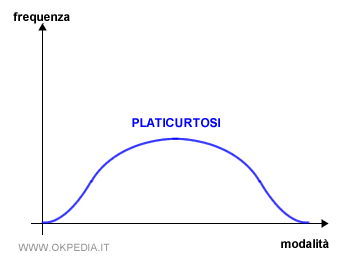
Le frequenze della distribuzione si distribuiscono quasi in modo uniforme nei valori nel campo di variazione.
La dispersione dei valori intorno alla media è molto ampia.
Esempio. La distribuzione dell'età dei lavoratori è platicurtica perché gran parte delle persone in età lavorativa ( 15-60 anni ) è occupato o cerca un'occupazione.
Il coefficiente di curtosi
Il coefficiente di curtosi (γ2) è un indice di misura del grado di curtosi di una distribuzione. È determinato dalla seguente formula.
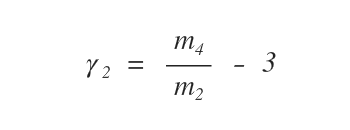
Dove m4 e m2 sono rispettivamente il momento centrale di ordine 4 e 2.
In base al coefficiente di curtosi si può stabilire il tipo di curtosi della distribuzione.
- se γ2 >0 la curva è leptocurtica ( appuntita )
- se γ2 =0 la curva è mesocurtica ( normale )
- se γ2 <0 la curva è platicurtica ( piatta )
Nota. In una distribuzione normale il coefficiente di curtosi è nullo.