Curva di frequenza
La curva di frequenza è la rappresentazione grafica della distribuzione delle frequenze delle classi. Data una popolazione suddivisa in classi statistiche con intervalli ben determinati e ogni classe è associata a una frequenza statistica.
La rappresentazione delle frequenze sul diagramma cartesiano disegna un poligono lisciato, la cui forma consente di comprendere più facilmente l'informazione significativa della distribuzione delle frequenze.
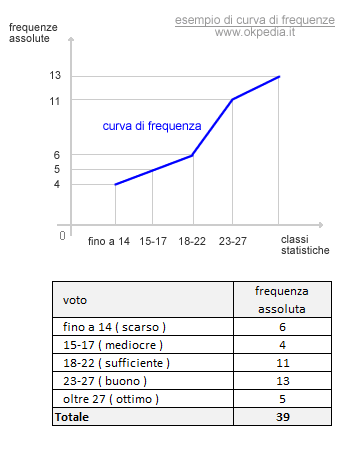
La suddivisione in classi statistiche ammorbidisce l'andamento della curva. Quanto più ampio è l'intervallo delle classi statistiche, tanto meno la curva di frequenza appare spigolosa. Per questa ragione la curva è anche detta poligono di frequenza lisciato.
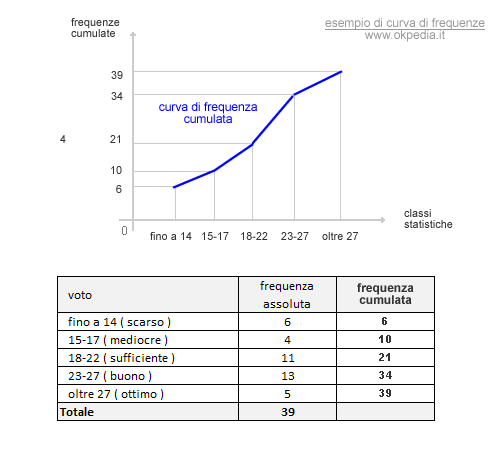
La curva di frequenza può essere utilizzata per rappresentare sia le frequenze ( assolute o relative ) di ciascuna classe che le frequenze cumulate o retrocumulate ( ogive ).
La curva di frequenza a campana
La curva di frequenza a campana è caratterizzata da una particolare forma con le frequenze crescenti fino a un valore centrale massimo e poi decrescenti. Questa forma è detta curva normale o curva gaussiana.
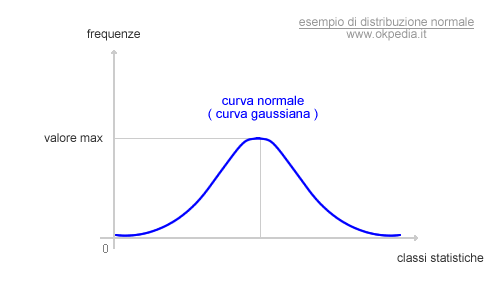
In una curva normale le modalità sono distribuite intorno a un determinato valore centrale massimo. Le frequenze sono equidistanti tra loro su entrambi i lati del valore centrale e la curva delle frequenze assume una forma perfettamente simmetrica, tendendo a zero su ambo i lati.
La curva di frequenza obliqua
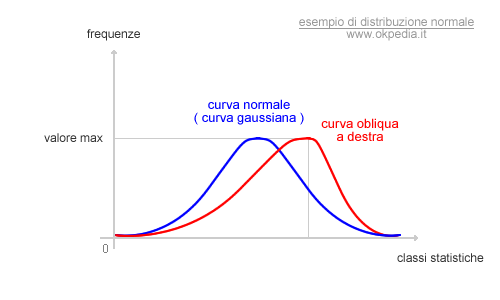
Quando la curva di frequenza non è simmetrica, il valore massimo si sposta da un lato e la curva ci appare obliqua con una lunga coda su un lato. Ad esempio, la seguente figura mostra una curva di frequenza obliqua a destra con una lunga coda sul lato sinistro.
Allo stesso modo, la curva di frequenza può essere obliqua a sinistra. In questo caso, il tratto lungo della curva si trova a destra, come nella seguente figura.
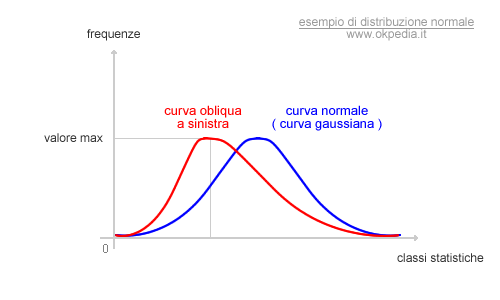
Le curve oblique caratterizzano le distribuzioni di frequenza asimmetriche. Ad esempio, la distribuzione del tasso di fertilità per fasce d'età è generalmente una curva di frequenza obliqua a sinistra poiché è molto alto nelle fasce d'età giovanili, cresce rapidamente a una determinata età e si riduce col passare del tempo.
La curva di frequenza ascendente e discendente
Quando il valore massimo della distribuzione coincide con un'estremità della curva, quest'ultima assume una forma continua discendente o crescente, a seconda se il valore massimo si trova sull'estremo iniziale o finale della distribuzione.
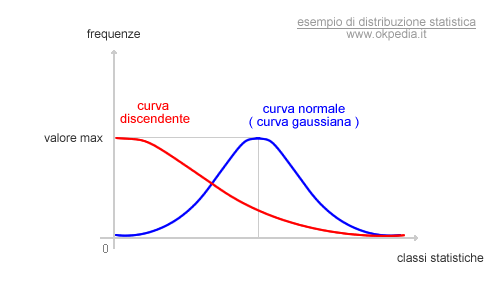
Nella precedente figura viene mostrato il caso di una curva di frequenza discendente. Il valore massimo si trova sull'estremo iniziale ( a sinistra ) della distribuzione.
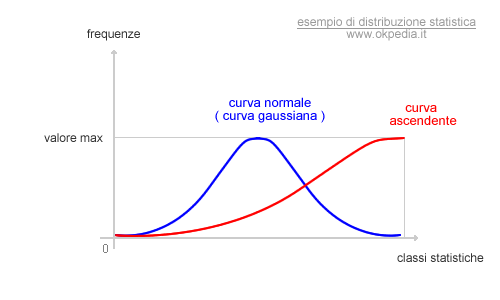
Nella precedente figura è, infine, rappresentato il caso della curva di frequenza crescente. In questo caso il valore massimo è situato nell'estremo finale ( a destra ) della distribuzione.
La curva di frequenza plurimodale
Le distribuzioni di frequenza sono dette plurimodali quando presentano due o più valori di picco assoluto massimo. Nella seguente figura è rappresentata una curva di frequenza bimodale.
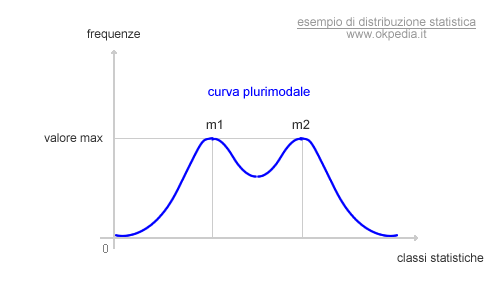
Come si può notare, la precedente distribuzione delle frequenze statistiche è caratterizzata da due valori massimi. Per questo motivo è detta bimodale. Più in generale, le curve con due o più picchi sono dette plurimodali o polimodali.
La curva di frequenza a U
In una curva di frequenza bimodale i valori massimi possono anche essere situati agli estremi della distribuzione statistica. In quest'ultimo caso particolare la curva di frequenza plurimodale assume una forma a U.
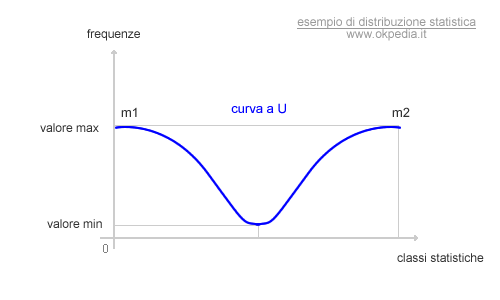
Nel tratto iniziale la curva è discendente. Una volta raggiunto il punto di minimo assoluto la curva diventa ascendente. Come si può agevolmente notare, i due punti di massimo sono ai margini estremi della distribuzione.
