Deviazione standard
In statistica la deviazione standard è un indicatore di dispersione di una distribuzione di valori. È anche detto scarto quadratico medio o scostamento quadratico medio ed è indicata con la lettera greca sigma ( σ ).
La formula della deviazione standard

Data una distribuzione statistica X composta da N valori numerici, la deviazione standard è la radice quadrata della media aritmetica degli scarti assoluti tra i valori della distribuzione { x1, x2, ... , xN} e un valore medio ( μ ).
Nota. In genere il valore medio è la media aritmetica ( μ ) della distribuzione X. Tuttavia, non necessariamente deve essere la media aritmetica. Può essere usata anche un'altra media ( es. geometrica ). A differenza delle altre medie, la media aritmetica ha la caratteristica di minimizzare la deviazione standard.
Se la deviazione standard ( σ ) è grande, i valori della distribuzione sono dispersi. Viceversa, se la deviazione standard è piccola, i valori sono concentrati vicino alla media.
Esempio di calcolo dello scostamento quadratico medio
La seguente distribuzione statistica X è formata da quattro valori ( x1, x2, x3, x4 ).
La media aritmetica ( μ ) della distribuzione X è uguale quindici ( μ=15 ).

Per calcolare lo scarto quadratico medio, si sommano i quadrati delle differenza assolute tra i singoli valori numerici ( 12, 13, 15, 20 ) e la media aritmetica ( μ=15 ) della distribuzione.
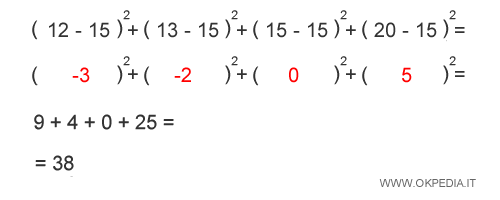
Si divide la somma per il numero degli elementi della distribuzione X ossia quattro (n=4).
In questo modo si ottiene la media aritmetica dei quadrati delle differenze.
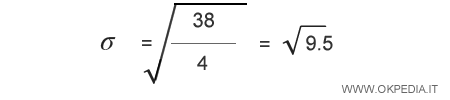
Infine si calcola la radice quadrata della media aritmetica dei quadrati.
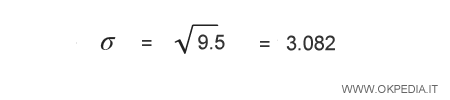
Il risultato è lo scostamento quadratico medio ( o deviazione standard ) della variabile statistica X.
In questo caso, lo scarto quadratico medio è circa 3,082.
La distribuzione standard nelle distribuzioni di frequenze
In una distribuzione di frequenze la deviazione standard si calcola moltiplicando il quadrato della differenza ( xi - μ )2 per la frequenza Φi della modalità.
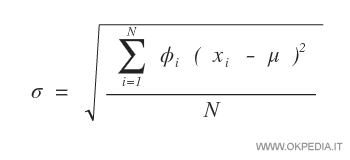
Nota. Nel caso in cui si tratti di classi con intervalli di valori, si prende come riferimento il valore centrale della classe.

Un esempio pratico di calcolo
Data la seguente distribuzione statistica X divisa in classi.
A ogni classe ( modalità ) è associata una frequenza assoluta ossia il numero delle volte che si ripete nella distribuzione.
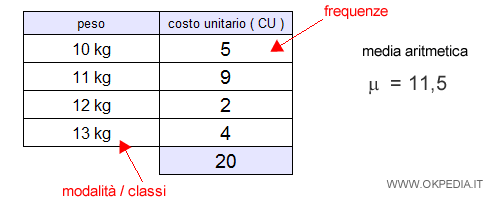
Poi si calcola la sommatoria dei quadrati delle differenze tra ogni modalità e la media aritmetica ( xi - μ )2 .
In questo caso ogni differenza è moltiplicata per la relativa frequenza Φi della classe.

Poi si divide la sommatoria dei quadrati per il numero della popolazione (N=20).
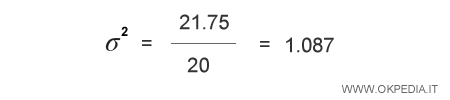
Infine si calcola la radice quadrata.
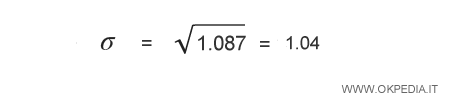
Si ottiene così lo scarto semplice medio della distribuzione.
Lo scarto quadratico medio di X è 1.041.
Le proprietà della deviazione standard
In una distribuzione normale il 68% degli elementi è compreso nell'intervallo ( μ-σ, μ+σ ).
Dove μ è il valore medio della distribuzione e σ la deviazione standard.
La percentuale dei casi osservati in una curva di distribuzione normale è la seguente:
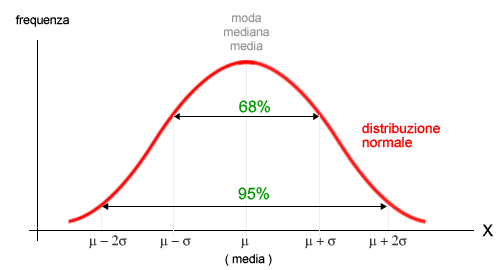
Nota. La percentuale degli elementi diventa il 95% se si prende in considerazione il doppio della deviazione standard ( μ-2σ, μ+2σ ). Sale al 99% se si considera il triplo ( μ-3σ, μ+3σ ). E così via.
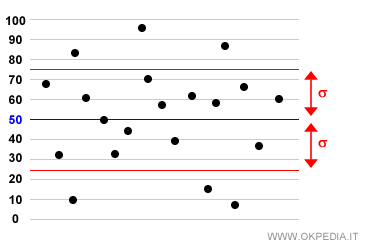
Ecco un esempio di distribuzione X composta da 20 elementi.
Dato lo scarto quadratico medio σ , 14 elementi sono compresi nell'intervallo ( μ-σ, μ+σ ) mentre 6 sono esterni.
Il teorema di Chebyshev estende questa proprietà della deviazione standard anche alle distribuzioni asimmetriche ( non normali ).
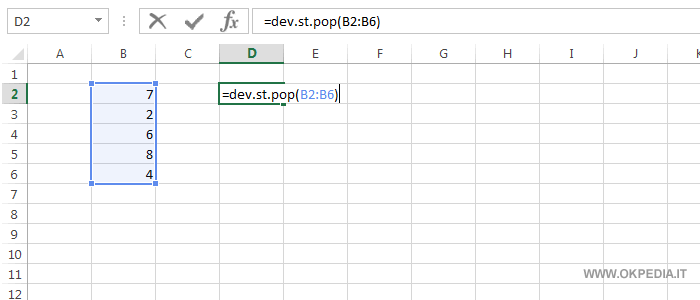
- Come calcolare la deviazione standard su Excel? Nel foglio di calcolo Excel la deviazione standard può essere calcolata tramite la funzione DEV.ST.POP