Coefficiente di variazione
Il coefficiente di variazione è un indicatore statistico di dispersione relativa, calcolato come rapporto tra la devianza standard e la media della distribuzione. È anche detto coefficiente di dispersione.
La formula del coefficiente di variazione
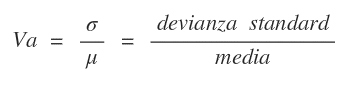
Cos'è la dispersione relativa? Si parla di dispersione relativa per indicare la variabilità di un fenomeno in termini percentuali. È usata per confrontare la variabilità dei fenomeni, senza prendere in considerazione l'unità di misura.
Un esempio pratico
Date due distribuzioni A e B, la prima misura il reddito nella Unione europea mentre la seconda il reddito negli Usa.
Per entrambe le distribuzioni viene calcolato il reddito medio μ ( media aritmetica ) e la devianza standard σ ( dispersione assoluta ).
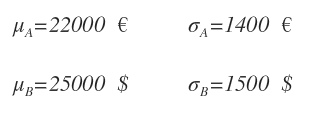
Le due distribuzioni usano un'unità di misura diversa, la prima utilizza l'euro e la seconda il dollaro.
Pertanto, i due indicatori di dispersione (σA e σB ) non sono confrontabili tra loro.
Nota. La devianza standard è un indicatore di dispersione assoluto. È influenzato dall'unità di misura e dalla dimensione del fenomeno statistico.
Per confrontare gli indicatori statistici occorre calcolare la dispersione relativa.
Si calcola il coefficiente di variazione ( o dispersione ) per entrambe le distribuzioni.
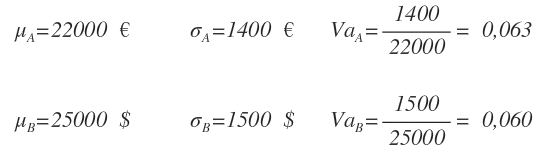
I coefficienti di variazione ( VaA e VaB ) sono comparabili tra loro.
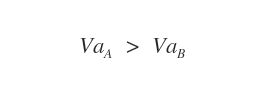
Pertanto, si può affermare che la dispersione relativa intorno al reddito medio è maggiore nella Ue rispetto agli Usa ( VaA > VaB ) .
I limiti del coefficiente di variazione
E' sconsigliato usare il coefficiente di variazione quando la media ha un valore molto vicino allo zero.
Essendo la media al denominatore del rapporto, un valore medio prossimo allo zero calcolerebbe un coefficiente di variazione troppo alto o tendente a infinito.
Pertanto, il dato perderebbe ogni significato e utilità pratica.
Domande e risposte
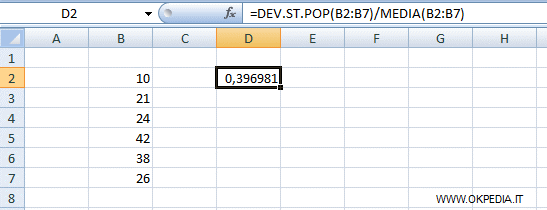
- Come calcolare il coefficiente di variazione sul foglio di calcolo?
Non c'è una funzione specifica. Su Excel o Calc il coefficiente di variazione si calcola con una formula tramite il rapporto tra la funzione dello scarto quadratico medio ( devianza standard ) e quella della media aritmetica ossia DEV.ST.POP / MEDIA.