Deviazione standard campionaria
La deviazione standard può essere calcolata anche in riferimento di un campione anziché dell'intera popolazione.
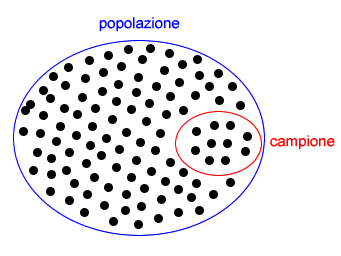
Tuttavia, la deviazione standard in un campione è tendenzialmente inferiore alla varianza calcolata sull'intera popolazione.
Nota. Questo accade perché il campione è composto da un minore numero di elementi rispetto alla popolazione. Pertanto, la dispersione statistica intorno al valore medio nel campione è naturalmente inferiore rispetto a quella dell'intera popolazione.
Per attenuare questo effetto, nel caso dei campioni viene usata la formula della deviazione standard campionaria.
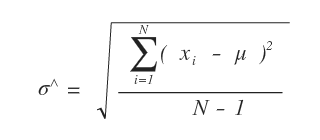
Questa formula è corretta per calcolare la deviazione standard in campione e ridurre le distorsioni rispetto a quella sull'intera popolazione.
Qual è la differenza nella deviazione standard campionaria? Nella formula della deviazione standard campionaria la somma delle differenze al quadrato viene divisa per N-1 anziché N.
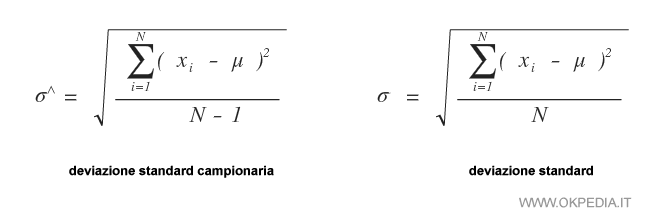
In questo modo, la deviazione standard campionaria calcolata in un campione tende a eguagliare la deviazione standard calcolata sull'intera popolazione.
Un esempio pratico
A volte è impossibile o antieconomico calcolare la deviazione standard sull'intera popolazione.
Esempio. Se una fabbrica produce migliaia di prodotti ogni ora, non può verificare la resistenza su tutti perché si rallenterebbe il processo produttivo. Inoltre, se il test di resistenza provocasse la distruzione del prodotto, sarebbe illogico farlo su tutte le unità prodotte.
In questi casi si calcola la deviazione standard su un singolo campione della popolazione.
Un campione è un gruppo di elementi estratti casualmente dalla popolazione.
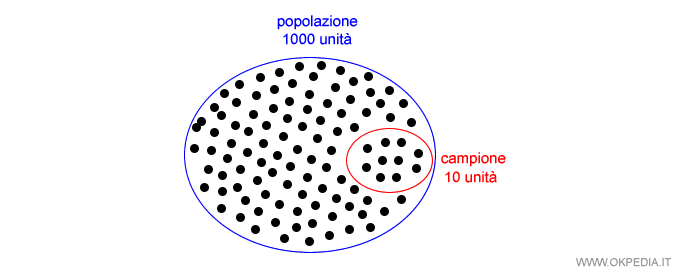
Esempio. La fabbrica produce 1000 unità di prodotto ogni ora. Un addetto estrae casualmente 10 unità prodotte per formare un campione. In questo caso il campione è formato dal 1% degli elementi della popolazione. Il campione viene destinato ai test di resistenza.
Si effettua il rilevamento di un'informazione su tutte le unità del campione ( es. resistenza ).

Poi si calcola la media aritmetica dei valori ( μ=10.5 ).
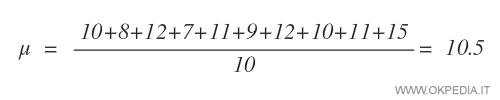
Per calcolare la variabilità dei valori intorno alla media (μ), si calcola la deviazione standard campionaria ( σ=2.27 ).
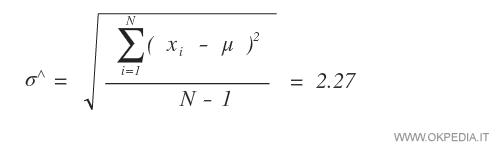
Dove xi sono i valori delle dieci unità del campione (N=10).
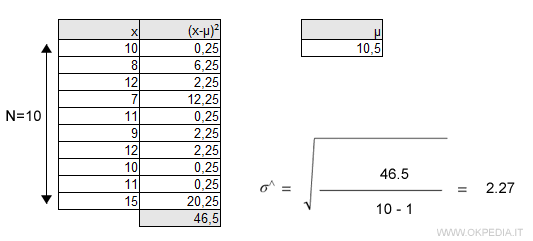
Nota. Se si calcolasse la dispersione intorno alla media del campione usando la formula della deviazione standard per l'intera popolazione, la variabilità risulterebbe inferiore e pari a 2.15. Il dato non sarebbe rappresentativo.
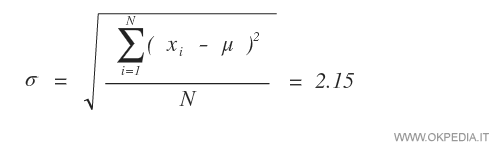
Secondo la statistica inferenziale, la media aritmetica ( μ=10.5 ) e la deviazione standard campionaria ( σ=2.27 ) sono simili a quelle che si otterrebbero sull'intera popolazione da cui è stato estratto il campione.
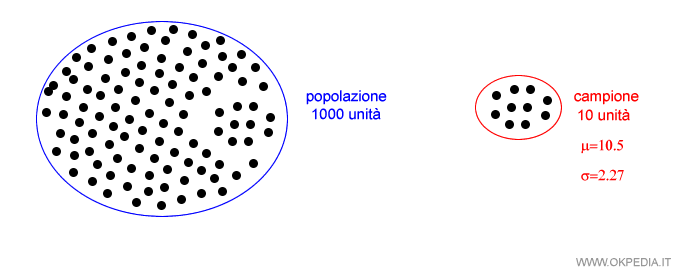
La fabbrica ha ottenuto una stima sulla resistenza dei prodotti fabbricati in un'ora analizzando soltanto quelli estratti nel campione rappresentativo.
Domande e risposte
- Come si calcola la deviazione standard campionaria su Excel?
Sul foglio di calcolo la funzione per calcolare la deviazione standard campionaria è DEV.ST
