Distribuzione multinomiale
Nella statistica la distribuzione multinomiale è una distribuzione di probabilità discreta di più variabili, quando sono soddisfatte le seguenti condizioni
- ogni prova ha più esiti possibili
- le prove sono indipendenti tra loro
- la probabilità p di ogni variabile in ogni prova è costante
La formula della distribuzione binomiale
La formula consente di calcolare la probabilità che si manifestino una serie di eventi specifici in N prove.
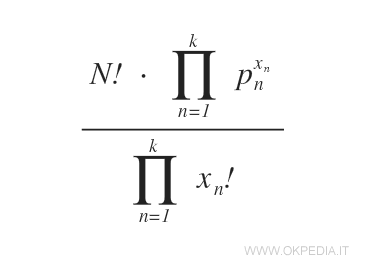
Dove N è la somma delle singole prove positive Xk di ogni k evento, mentre Pk è la probabilità semplice di ogni k evento.
Nota. La distribuzione multinomiale è la generalizzazione della distribuzione binomiale su più variabili, nel caso in cui ogni variabile fornisca più di due risultati.
Un esempio pratico
Un'urna contiene 10 palline, di cui 2 gialle, 5 blu e 3 rosse.
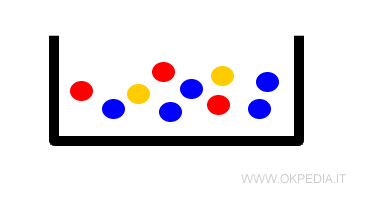
Una persona estrae una pallina per sei volte (N=6) e dopo ogni estrazione reinserisce la pallina nell'urna.
Qual è la probabilità di estrarre tre palline blu, due rosse e una gialla?
In questo caso gli eventi sono tre (k=3).
La probabilità semplici degli eventi in ogni prova sono le seguenti:
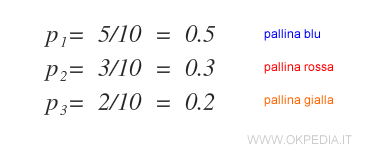
Nota. Trattandosi di un'estrazione con reinserimento, la probabilità di estrarre una pallina dello stesso colore è sempre la stessa in ogni prova. Quindi le prove sono indipendenti tra loro.
Gli eventi devono verificarsi un determinato numero di volte durante le prove:

Quindi N=X1+X2+X3=6
Applicando la formula della distribuzione multinomiale si calcola la probabilità degli eventi
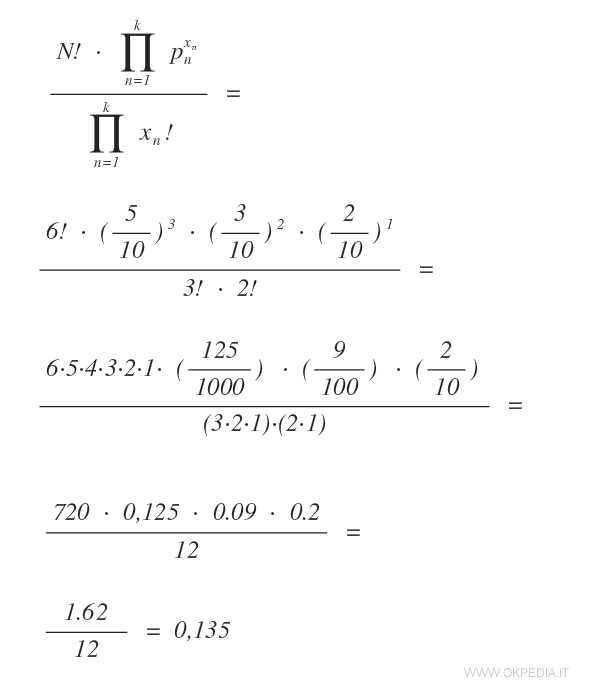
La probabilità di estrarre tre palline blu, due rosse e una gialla in sei estrazioni è del 13,5% ossia p=0.135.
Nota. Nel calcolo abbiamo omesso di fare semplificazioni algebriche per rendere più lineare la spiegazione. Nella pratica è comunque consigliato semplificare laddove possibile, prima di svolgere i calcoli.
