Gli integrali
Gli integrali sono un'operazione fondamentale del calcolo infinitesimale. Il simbolo dell'integrale di una funzione è il seguente.
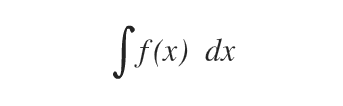
La funzione f(x) è detta funzione integranda.
La differenza tra integrali definiti e indefiniti. Nello studio degli integrali occorre distinguere tra integrali definiti e integrali indefiniti perché esprimono concetti diversi pur avendo lo stesso nome.
I tipi di integrali
Esistono due tipi di integrali.
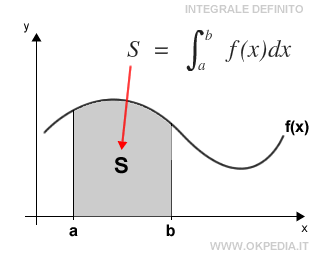
- Integrale definito. L'integrale definito di una funzione è il numero reale che misura la superficie della figura delimitata dal grafico della funzione.
- Integrale indefinito. L'integrale indefinito di una funzione f(x) è una famiglia di funzioni primitive F(x) la cui derivata F'(x) è uguale alla funzione f(x). È l'operazione inversa della derivata.

Nota. Pur avendo lo stesso nome, l'integrale definito e indefinito sono concetti diversi, rispondo a problemi differenti e vanno studiati separatamente. Tuttavia, c'è una stretta relazione tra l'integrale definito e la funzione primitiva F(x). Quindi, il calcolo di un integrale definito può essere ricondotto a quello di un integrale indefinito, in quanto è più diretto e rapido.
L'origine del calcolo integrale
Nonostante gli integrali siano generalmente l'ultimo capitolo nello studio del calcolo infinitesimale, dopo i limiti e le derivate, gli integrali sono i primi ad essere stati usati dall'uomo.
I primi calcoli sugli integrali risalgono al mondo antico, quando nel III secolo a.C. i matematici greci ( Archimede di Siracusa ) cercano di calcolare la quadratura delle figure geometriche piane, anticipando il concetto di integrale definito.
Lo studio viene ripreso alla fine del medioevo da diversi matematici europei, tra i quali Simon Stevin, Bonaventura Cavalieri, John Wallis, Nicolaus Mercator e Pierre de Fermat.
Il concetto di integrale indefinito nasce nel XVII secolo insieme con gli studi sulle derivate di Isaac Newton, Johann Bernoulli e Gottfried Wilhelm von Leibniz.
A Leibniz si deve anche la nascita dei termini integrazione e derivazione.
Le definizioni moderne di integrale risalgono, invece, al XIX secolo con gli studi di Johann Peter Gustav Lejeune Dirichlet e Georg Friedrich Bernhard Riemann.
