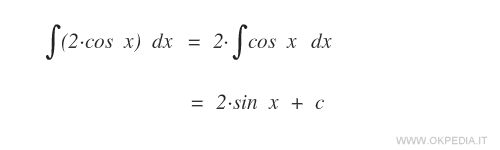Le proprietà degli integrali indefiniti
Gli integrali indefiniti sono l'operazione inversa della derivata di una funzione. Alcune proprietà degli integrali indefiniti sono particolarmente utili da ricordare perché agevolano le operazioni del calcolo infinitesimale.

Le principali proprietà degli integrali indefiniti sono le seguenti:
La derivata di un integrale
La derivata di un integrale è la funzione stessa.
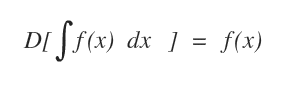
Dimostrazione
L'integrale della funzione f(x) è una funzione primitiva F(x) la cui derivata restituisce f(x).
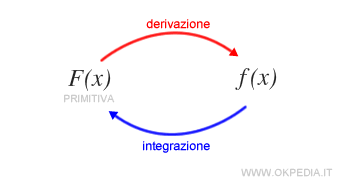
Pertanto, la derivata di un integrale della funzione f(x) è la funzione f(x) stessa.
Teorema della condizione sufficiente di integrabilità
Se una funzione f(x) è continua nell'intervallo [a,b], allora ammette delle primitive F(x) nello stesso intervallo.
Da questo teorema si deduce che tutte le funzioni continue sono integrabili.
Tuttavia, non tutte le funzioni continue sono derivabili.
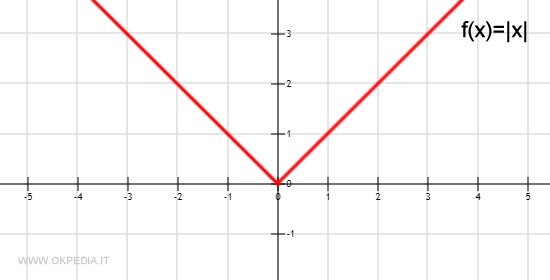
Esempio. La funzione f(x)=|x| è continua ma non è derivabile in x=0, perché in questo punto il limite destro e sinistro della derivata f'(x) per x→0 sono diversi quindi non ha una derivata in x=0. Tuttavia, nel punto x=0 la funzione f(x) ammette comunque infinite primitive ossia è integrabile.
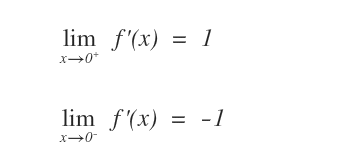
Perché? Nel punto x=0 la funzione continua f(x)=|x| è integrabile ma non derivabile a causa della presenza di un punto angoloso. Nei punti angolosi la funzione non è derivabile ma resta comunque una funzione continua.
Prima proprietà di linearità dell'integrale
Date due funzioni f(x) e g(x) che ammettono rispettivamente le primitive F(x) e G(x), allora anche la funzione f(x)+g(x) ammette una primitiva ed è uguale a F(x)+G(x).
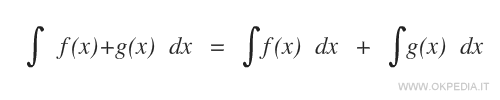
Questa proprietà è una conseguenza della proprietà delle derivate. La derivata della funzione f(x)+g(x) è uguale alla somma delle derivate f'(x)+g'(x).
Dimostrazione
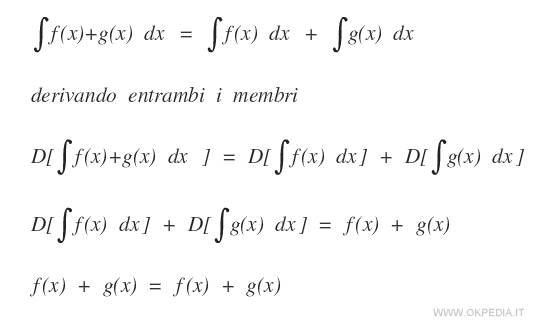
Esempio
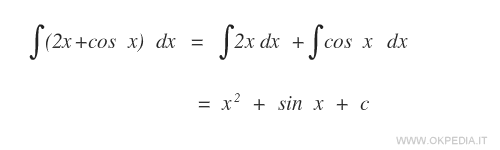
Seconda proprietà di linearità dell'integrale
Se una funzione f(x) ammette una primitiva F(x), allora anche la funzione k·f(x) ammette una primitiva ed è k·F(x).
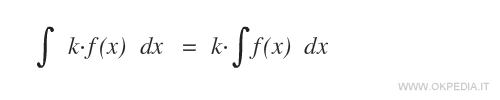
Questa proprietà ha origine dalla derivata di una funzione per una costante k. La derivata di k·f(x) è uguale a k·f'(x).
Dimostrazione
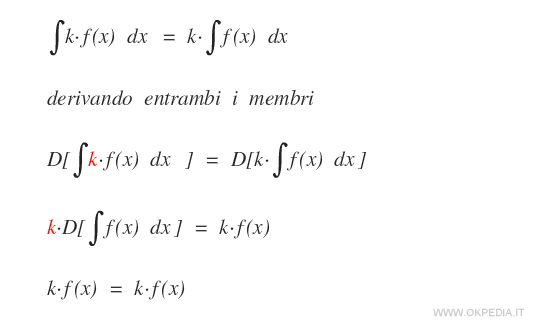
Esempio