Integrazione per sostituzione

L'integrazione per sostituzione è un metodo di risoluzione degli integrali, indefiniti o definiti, quando non sono risolvibili in modo immediato. Tramite il metodo per sostituzione si definisce una variabile t per riscrivere l'integrale in una forma più semplice e risolvibile.

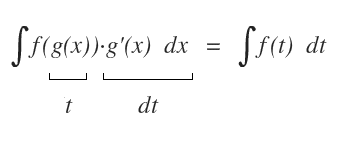
Come calcolare l'integrale per sostituzione


1. Si pone t=g(x)
2. Si pone dt=g'(x) dx oppure dx=g'(t) dt
3. Si calcola l'integrale rispetto alla variabile t
4. Si riscrive la primitiva in funzione di x

I due metodi di integrazione per sostituzione

Per risolvere un integrale per sostituzione si possono seguire due metodi equivalenti e alternativi tra loro.

Quale metodo scegliere?

La convenienza a scegliere il primo metodo o l'altro dipende dai calcoli da svolgere.

Entrambi i metodi di integrazione conducono allo stesso risultato.

Nota. Generalmente, il primo metodo è più rapido se g'(x)dx è evidente nella funzione. Il secondo metodo richiede alcuni passaggi in più ma, in compenso, consente di calcolare direttamente il dx e di sostituirlo, senza dover cercare g'(x)dx nell'integrale.

Un esempio pratico

Il seguente integrale è risolto con entrambi i metodi.

Il processo di calcolo cambia ma il risultato è identico.

Esempi di integrazione per sostituzione

Esempio 1

Il seguente integrale non è immediatamente risolvibile, perché non corrisponde a nessun integrale elementare.

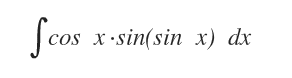
Tuttavia, l'integrale rispetta le caratteristiche della formula generale per integrazione.

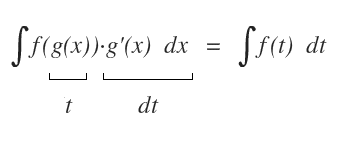
In quanto

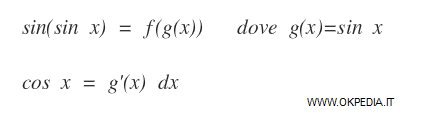
Assegniamo alla variabile t la funzione sin x.

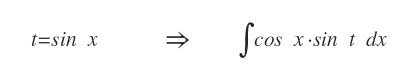
Poi deriviamo la variabile t rispetto a x (dx).

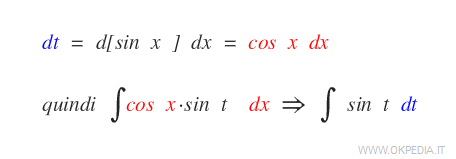
Come si può notare dt = g'(x) dx ossia dt = d(sin x) dx = cos x dx

E' quindi possibile riscrivere l'integrale in una forma più semplice sostituendo cos x dx con dt.

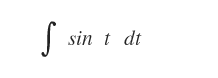
Dopo la sostituzione l'integrale è facilmente calcolabile, perché si tratta di un integrale elementare.

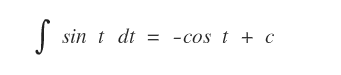
A questo punto è sufficiente sostituire la variabile t con sin x

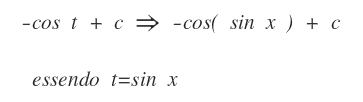
Si ottiene così il risultato dell'integrale.

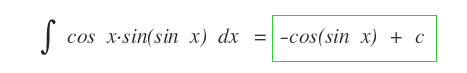
Esempio 2

La seguente funzione non è integrabile in modo immediato.

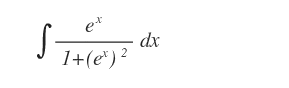
Tuttavia, si può semplificare ponendo t=e^x.

Poi calcolare il differenziale dt e sostiuirlo a e^x dx.

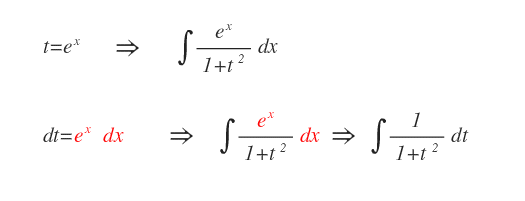
In questa forma equivalente l'integrale è risolvibile immediatamente perché si tratta di un integrale elementare.

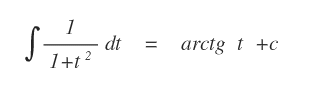
Ora si può sostituire la variabile t con e^x.

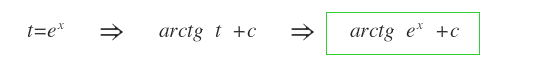
Si ottiene così il risultato dell'integrale.

Altri esercizi svolti

Per vedere altri esempi ed esercizi con il metodo di integrazione per sostituzione.