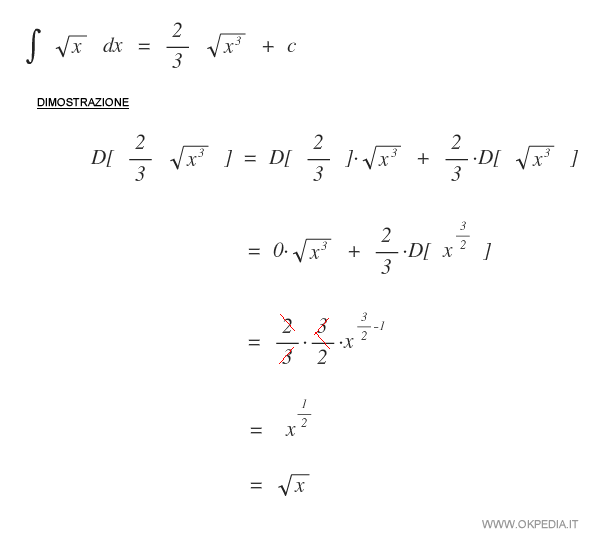Integrali di funzioni elementari
Le seguenti regole di integrazione consentono di calcolare velocemente la primitiva delle principali funzioni elementari.
Elenco di primitive delle funzioni elementari
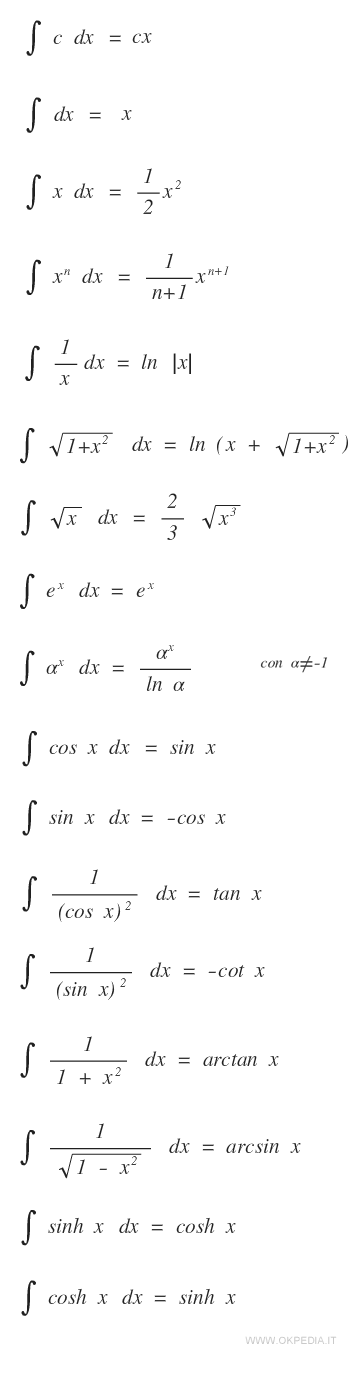
La precedente tabella mostra le funzioni primitive delle principali funzioni elementari f(x). Una volta memorizzata, la tabella consente di svolgere più velocemente il calcolo dell'integrale di una funzione.
Come si calcola l'integrale di una funzione elementare? Nei prossimi paragrafi sono pubblicate le spiegazioni e le dimostrazioni matematiche del calcolo della primitiva di alcune funzioni elementari.
L'integrale di una costante
L'integrale di una costante k è la funzione primitiva kx
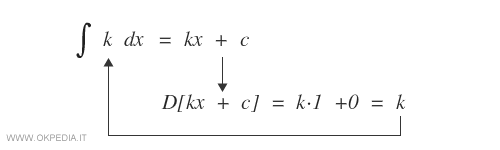
Dimostrazione
La derivata di kx è uguale a k.
Quindi, kx è una primitiva della funzione k.
L'integrale di dx
L'integrale di dx è il seguente:
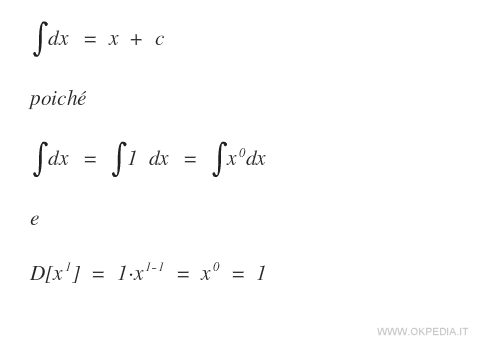
L'integrale di dx è l'integrale di 1 e la derivata della funzione f(x)=x è uguale a 1.
L'integrale di X
L'integrale della potenza x è il seguente:
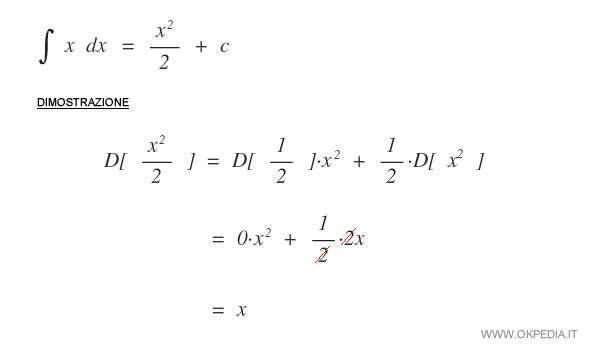
L'integrale della potenza
L'integrale della potenza xn è il seguente:
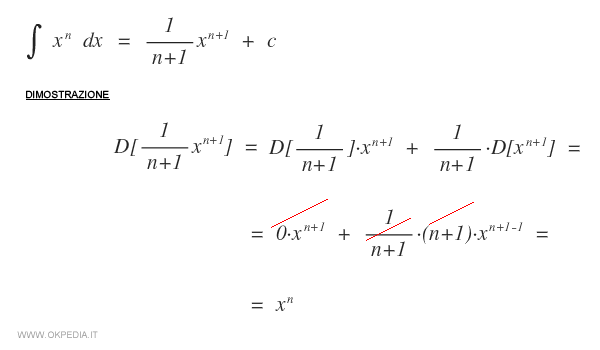
La derivata di 1/(n+1)xn+1 è uguale a xn. Pertanto, xn è una primitiva della potenza xn.
L'integrale della radice
La dimostrazione dell'integrale della radice di x è la seguente: