Integrale definito
L'integrale definito di una funzione f(x) in un intervallo [a,b] è un numero reale che misura l'area S compresa tra la funzione e l'asse delle ascisse, delimitata dai due segmenti verticali che congiungono gli estremi [a,b] al grafico della funzione.
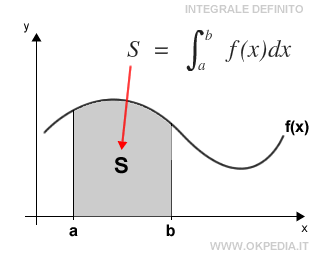
La funzione f(x) è detta funzione integranda nell'intervallo di integrazione [a,b].
L'integrale definito è un numero reale positivo se il grafico si trova al di sopra dell'asse orizzontale delle ascisse (x). Viceversa, l'integrale definito è un numero reale negativo se si trova il grafico al di sotto delle ascisse.
La spiegazione dell'integrale definito
In geometria l'integrale definito è utilizzato per calcolare l'area di una figura geometrica curvilinea.
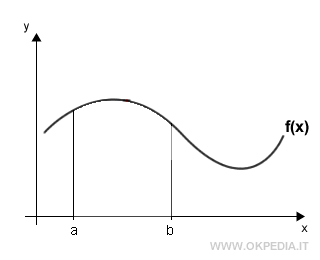
Per calcolare l'area tra il grafico di una funzione e l'ascisse in un intervallo chiuso [a,b] si suddivide la basa in intervalli più piccoli [xi,xi+1] di ampiezza costante Δx.
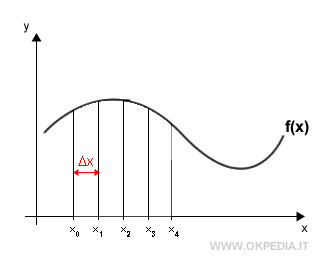
Ciascun intervallo ha un valore minimo mi e un valore massimo Mi.
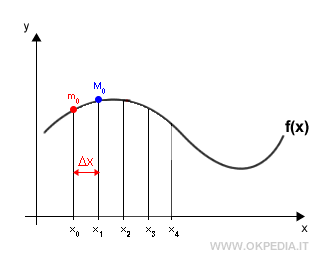
Quindi, per ogni intervallo [xi,xi+1] è possibile calcolare l'area del rettangolo fino al valore minimo miΔxi e l'area del rettangolo fino al valore massimo MiΔxi.
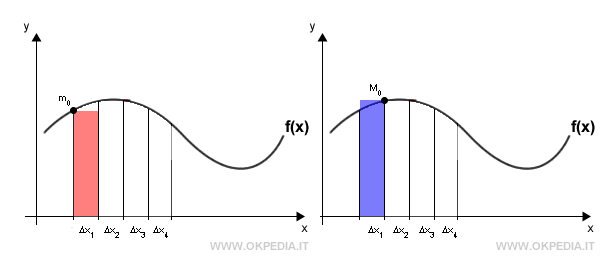
Sommando le superfici dei rettangoli si ottengono due aree:
- La somma inferiore s è la somma delle aree degli intervalli miΔxi.
- La somma superiore S è la somma delle aree degli intervalli MiΔxi.
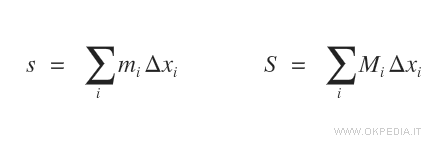
L'area della figura curvilinea è compresa tra la somma inferiore s e la somma superiore S.
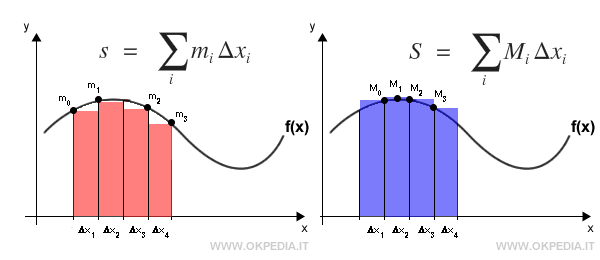
Facendo tendere a zero gli intervalli [xi,xi+1] ( le basi dei rettangoli ) la somma inferiore e superiore convergono all'integrale definito I, ossia all'area della figura curvilinea.
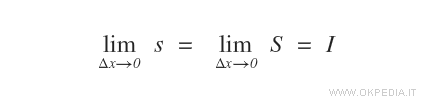
Al ridursi della base Δx i rettangoli diventano sempre più piccoli, riducendo la presenza delle superfici in difetto o in eccesso intorno al grafico.
L'integrale definito della funzione f(x) nell'intervallo [a,b] è indicato con la seguente notazione
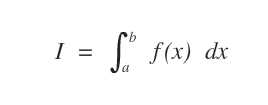
Il simbolo dell'integrale ∫ rappresenta la somma dall'estremo sinistro (a) all'estremo destro (b) delle aree dei rettangoli.
L'area di ogni rettangolo è determinata da f(x)·dx, dove f(x) identifica l'altezza e dx la larghezza (base) dei rettangoli infinitesimali.
Come calcolare l'integrale definito
Se la funzione f(x) è continua nell'intervallo [a,b], l'integrale definito è uguale alla differenza tra la primitiva F(b) e la primitiva F(a) della funzione.
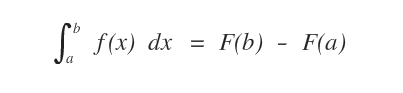
In pratica, l'integrale definito è l'incremento di una qualsiasi funzione primitiva di f(x) dall'estremo sinistro (a) all'estremo destro (b).
Nota. Per il calcolo si può scegliere una qualsiasi tra le infinite primitive F(x)+k della funzione f(x) in quanto la costante k si annulla da sé con la sottrazione F(b)+k-[F(a)+k].
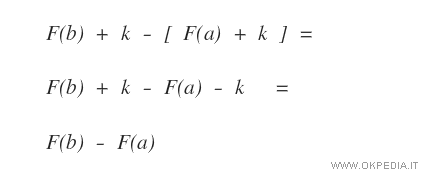
In questo modo, è possibile calcolare l'integrale definito usando le stesse regole di calcolo degli integrali indefiniti.
Esempio di calcolo dell'integrale definito
La seguente funzione traccia un arco di parabola sull'ascisse dall'estremo a=0 all'estremo b=8.
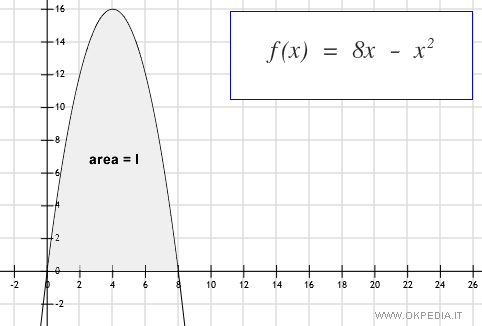
Per misurare la superficie della figura si calcola l'integrale definito della f(x) nell'intervallo [0,8].

Pertanto l'area della figura è 85.4.
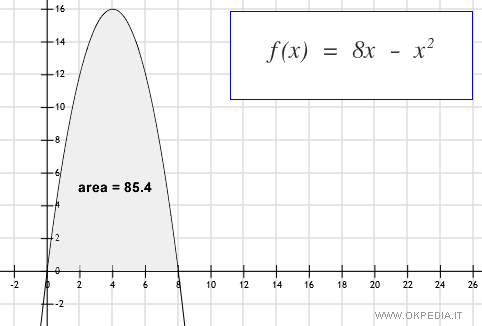
In questo modo abbiamo calcolato l'area della figura curvilinea tramite l'integrale definito della funzione f(x) nell'intervallo [0,8].
Teoremi degli integrali definiti
Primo teorema
Una funzione continua f(x) in un intervallo [a,b] è integrabile in [a,b]
Secondo teorema
Una funzione f(x) monotona e limitata in un intervallo [a,b] è integrabile in [a,b]
Proprietà degli integrali definiti
Le principali proprietà degli integrali definiti sono le seguenti:
- Data una funzione f(x) continua nell'intervallo [a,b] e la sua funzione primitiva F(x), l'integrale definito è uguale alla differenza tra le funzioni primitive F(b)-F(a).
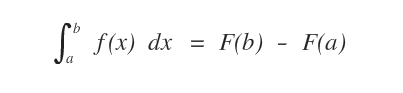
Nota. Questa proprietà permette di calcolare l'integrale definito tramite l'incremento delle primitive di F(x) in un intervallo.
- Se due funzioni f(x) e g(x) integrabili nell'intervallo [a,b], allora anche la somma f(x)+g(x) è integrabile in [a,b].
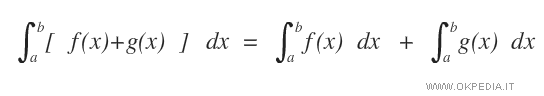
Questa proprietà è detta proprietà additiva rispetto alla funzione integranda
- Se la funzione f(x) è integrabile nell'intervallo [a,b] e k è una costante qualsiasi, allora anche la funzione kf(x) è integrabile.
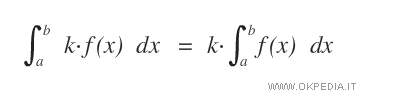
- Se la funzione f(x) è integrabile nell'intervallo [a,b] e a≤c≤b, allora la funzione f(x) è integrabile negli intervalli [a,c] e [c,b].
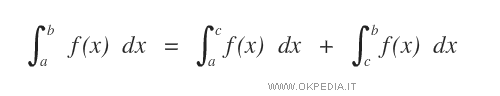
Questa proprietà è detta proprietà additiva dell'integrale definito rispetto all'intervallo di integrazione.
